PREMIÈRE PARTIE : ALGÈBRE

Nous abordons maintenant notre troisième leçon de mathématiques. Il est composé de deux parties importantes.

La première est consacrée à l'algèbre. Vous connaîtrez ce qu'est une expression algébrique et apprendrez à effectuer des calculs sur les monômes et les polynômes. Vous verrez ensuite ce qu'est une équation et comment la résoudre.

Dans la seconde partie, il sera question des logarithmes. Vous verrez que par leur intermédiaire les calculs complexes avec les puissances et les extractions de racine se transforment en simples multiplications ou divisions.

D'autre part, comme vous êtes maintenant habitués aux développements mathématiques, nous les emploierons désormais de préférence aux explications littérales toujours plus longues et moins précises.

Enfin, comme nous l'avons déjà dit et répété dans les deux premières leçons, nous vous invitons à refaire les exercices cités en exemples, tant au cours de vos lectures que quelque temps après.

 

1. 1. DÉFINITION

On appelle expression algébrique, un ensemble de lettres et de nombres reliés entre eux par des signes indiquant les opérations à effectuer.

Exemple :

 

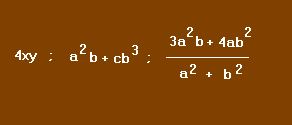
Chaque lettre représente un nombre. Si la même lettre figure plusieurs fois dans la même expression, elle y représente le même nombre. Pour obtenir la valeur numérique de l'expression, il suffit de remplacer chaque lettre par le nombre qu'elle représente.

Exemple : calculez la valeur numérique de :

 

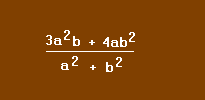
Lorsque a = 1 et b = 2

Nous écrivons :

Il faut du soin et de l'attention. Tout ce qui se trouve dans une parenthèse, devra être considéré un nombre unique à prendre comme tel, après l'avoir calculé.

La règle des signes, que nous avons vu, s'applique évidemment dans ces calculs. D'autre part, la règle concernant la suppression des parenthèses précédées du signe + ou - s'applique également :

Exemple : si a = 1 et b = 2, on obtient :

Les deux premières expressions qui ne diffèrent que par des parenthèses et des signes ont, comme vous le voyez, des valeurs numériques différentes.

1. 3. 1. - EXPRESSION ALGÉBRIQUE DITE ENTIÈRE

L'expression ne contient pas de lettres au dénominateur.

Exemple :

1. 3. 2. - EXPRESSION ALGÉBRIQUE DITE FRACTIONNAIRE

L'expression contient des lettres au dénominateur.

Exemple :

1. 3. 3. - Monômes

L'expression ne contient pas de signes d'addition ou de soustraction.

Exemple :

1. 3. 4. - POLYNÔMES

L'expression contient des signes d'addition ou de soustraction entre plusieurs monômes.

Exemple :

2. 1. - ÉCRITURE D'UN MONÔME

Étant donné qu'un monôme est un produit de facteurs, et que l'on peut intervertir l'ordre de ses facteurs, sans changer le résultat, il faut toujours s'arranger pour réduire les monômes sous une forme condensée plus facilement utilisable :

Exemple :

Un monôme est composé de deux partie :

• Un facteur numérique que l'on appelle coefficient ;
• Un produit de facteurs littéraux que l'on appelle partie littérale.

Exemples :

3a²b ---------------» 3 est le coefficient et a²b est la partie littérale ;

a²b ----------------» 1 est le coefficient et a²b est la partie littérale ;

- a²b --------------» - 1 est le coefficient et a²b est la partie littérale.

(Pour les deux dernières expressions, le coefficient 1 est sous-entendu).

2. 2. 1. - DEGRÉ D'UN MONÔME PAR RAPPORT A UNE LETTRE

Définition : On appelle degré d'un monôme par rapport à une lettre, l'exposant de cette lettre dans ce monôme.

3a²b est de degré 2 pour (a) et de degré 1 pour b.

x³y⁴ est de degré 3 pour (x) et de degré 4 pour y.

2. 2. 2 . - DEGRÉ D'UN MONÔME PAR RAPPORT A UN ENSEMBLE DE LETTRES

Définition : On appelle degré d'un monôme par rapport à l'ensemble des lettres, la somme des exposants de toutes ses lettres.

Le monôme 2a²bx³y⁴ est de degré 10 (2 + 1 + 3 + 4) pour l'ensemble de ses lettres.

2. 3. - MONÔMES SEMBLABLES

Définition : Des monômes semblables sont des monômes qui ont même partie littérale.

Exemples :

Il en découle tout de suite que la somme de plusieurs monômes semblables est un monôme semblable dont le coefficient est la somme des coefficients des monômes :

C'est ce que l'on appelle réduire les monômes semblables.

2. 4. 1. - PRODUIT DE PLUSIEURS MONÔMES

Le produit de plusieurs monômes est un monôme :

- dont le coefficient est le produit des coefficients des monômes donnés ;

- dont la partie littérale comprend les lettres contenues dans les monômes, chacune d'elles étant affectée d'un exposant égal à la somme de ses exposants dans les facteurs.

Exemple :

2. 4. 2. - QUOTIENT DE MONÔMES

Le quotient d'un monôme par un monôme s'écrit sous la forme d'une fraction qu'il faut simplifier au maximum.

exemples :

On a simplifié numérateur et dénominateur par le terme commun b.

On a simplifié numérateur et dénominateur par 2ab²c².

Remarque : Un monôme A est divisible par un nombre B, lorsque A contient toutes les lettres de B avec des exposants aux moins égaux.

Exemples :

3. 1. - DÉFINITIONS

3. 1. 1. - POLYNÔME

Un polynôme est une somme de plusieurs monômes qui sont les termes du polynôme.

Exemples :

3. 1. 2. - BINÔME

On appelle binôme, un polynôme qui ne contient que deux termes.

Exemple : 3a + 4b

3. 1. 3. - TRINÔME

On appelle trinôme, un polynôme qui ne contient que trois termes.

Exemple : 2x² - 3xy + 4y²

3. 2. - RÉDUCTION DE POLYNÔMES

Il faut toujours commencer par rendre le polynôme le plus simple possible.

Exemple :

En réduisant, on trouve :

Le polynôme réduit s'écrira donc : 5x³ + x²y + 4xy² dont la forme est quand-même plus simple que celle proposée ci-dessus.

Remarque : Il est de règle d'écrire un polynôme de manière que les degrés de ses termes, par rapport à une de ses lettres, aillent soit en diminuant, soit en augmentant.

Exemples :

- 8ax³ + 6bx² + 3cx est ordonné par rapport aux puissances décroissantes de x.

- 3 + 2xy + (4 / 3) . xy² - 6y³ est ordonné par rapport aux puissances croissantes de y.

D'autre part, on peut ordonner un polynôme (ou un monôme) en fonction de l'ordre alphabétique de ses lettres.

Exemples :

Au lieu de : 3ayx + 4yxz - 3bac

On écrira : 3axy + 4xyz - 3abc

et mieux : - 3abc + 3axy + 4xyz

3. 3. - DEGRÉ D'UN POLYNÔME

Définition : Le degré d'un polynôme par rapport à une lettre est l'exposant le plus élevé de cette lettre dans le polynôme.

3. 3. 1. - POLYNÔME A UNE SEULE LETTRE

Exemples :

3. 3. 2. - POLYNÔME A PLUSIEURS LETTRES

Exemples :

3. 4. - OPÉRATIONS SUR LES POLYNÔMES

3. 4. 1. - ADDITION DE POLYNÔMES

Règle : La somme de plusieurs polynômes s'obtient en écrivant les termes des polynômes les uns à la suite des autres et en réduisant les termes semblables du polynôme obtenu.

Exemple :

(x⁴ + 3x²y² + 3y) + (3x⁴ + 2x²y³ + 5y) = x⁴ + 3x²y² + 3y + 3x⁴ + 2x²y³ + 5y = x⁴ + 3x²y² + 2x²y³ + 8y

3. 4. 2. - SOUSTRACTION DE POLYNÔMES

Règle : Pour retrancher un polynôme, on ajoute les termes de ce polynôme changés de signe.

Exemples :

3. 4. 3. - PRODUIT D'UN POLYNÔME PAR UN MONÔME

Règle : Pour multiplier un polynôme par un monôme, on multiplie successivement chaque terme du polynôme par le monôme. C'est le produit d'une somme par un nombre.

Exemple :

3. 4. 4. - PRODUIT D'UN POLYNÔME PAR UN POLYNÔME

Un polynôme étant la somme de plusieurs monômes, on appliquera la règle de la multiplication d'une somme par une somme.

Règle : Pour multiplier deux polynômes entre eux, on multiplie chaque terme de l'un successivement par chaque terme de l'autre et on ajoute algébriquement les produits obtenus. Ensuite on réduit les termes semblables.

Exemple :

Et en réduisant : 2a²b² + a²b - ab² - 6a² + 5ab - b²

3. 4. 5. - PRODUITS REMARQUABLES

Il y a quelques produits remarquables qu'il est souhaitable de connaître par cœur.

Carré de la somme de deux nombres :

Carré de la différence de deux nombres :

Produit de la somme de deux nombres par leur différence :

D'autres produits remarquables sont importants :

et

ainsi que

et

Remarque : L'utilisation des produits remarquables conduit souvent à la décomposition d'un polynôme en produits de facteurs plus simples qui sont susceptibles de réductions ultérieures.

Prenons un exemple, soit :

 

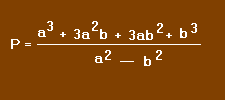
Le numérateur et le dénominateur sont des produits remarquables. Nous pouvons donc écrire :

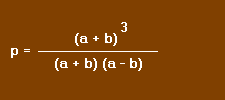
et en simplifiant par a + b nous trouvons :

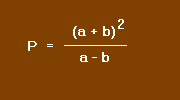
Expression plus simple que celle proposée.

3. 4. 6. - DIVISION D'UN POLYNÔME PAR UN MONÔME

Le quotient du polynôme P = 10x³ - 4x²y + 6xy² par le monôme 2x est le polynôme qu'il faut multiplier par 2x pour obtenir le polynôme P. On écrit :

   

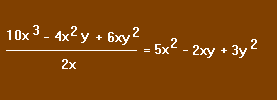
Un polynôme est donc divisible par un monôme lorsque tous les termes de ce polynôme sont divisibles par ce monôme.

Règle : Pour diviser un polynôme par un monôme, on divise tous les termes de ce polynôme par le monôme.

Application :

1 - Mise en facteur commun.

Considérons le polynôme :

Tous ses termes étant divisibles par 5a, on peut l'écrire sous la forme :

On dit que le monôme (5a) a été mis en facteur commun dans le polynôme.

Le monôme de plus haut degré pouvant être mis en facteur dans un polynôme comprend les lettres communes à tous les termes, chaque lettre étant affectée du plus petit exposant qu'elle a dans le polynôme. Le coefficient du monôme mis en facteur peut être arbitraire (exemple 1), mais on prend le plus souvent pour coefficient le plus grand commun diviseur des coefficients des termes (exemple 2).

Exemple 1 :

Nous avons pris (x) comme facteur commun, alors que nous aurions pu prendre xy.

Exemple 2 :

2 - Décomposition d'un polynôme en un produit de facteurs.

Cette décomposition est possible :

a - mettant un monôme en facteur commun

b - en groupant les termes du polynôme de manière à pouvoir effectuer ensuite des mises en facteur commun.

Exemple :

Mettons (b) en facteur commun dans la première somme et (y) en facteur commun dans la seconde :

Mettons (a + x) en facteur :

c - en appliquant les propriétés des produits remarquables.

Exemple 1 :

Exemple 2 :

Exemple 3 :

------------------------------------------------------» = (x + y)² - z² ; application de (a + b)²

------------------------------------------------------» = (x + y + z) (x + y - z) ; application de (a + b) (a - b)

La décomposition des polynômes en produits de facteurs est souvent appliquée à la simplification des fractions.

4. 1. - INTRODUCTION A LA NOTION D'ÉQUATION

1 - Quand vous écrivez 3 + 7 = 7 + 3, vous obtenez une égalité numérique. Vous pouvez d'ailleurs la vérifier rapidement, en effectuant les calculs indiqués de part et d'autre du signe = et en vous assurant que les résultats trouvés sont les mêmes.

2 - Si vous écrivez maintenant 3x + 7 = 7 + 3x, vous obtenez une identité littérale (remarquez qu'en remplaçant (x) par une valeur numérique quelconque, vous retrouvez une égalité numérique).

Définition de l'identité : Une identité est une égalité littérale qui est vérifiée pour toutes les valeurs numériques que l'on peut donner aux lettres qu'elle renferme.

Exemple : Reprenons l'identité 3x + 7 = 7 + 3x et donnons à (x) les valeurs suivantes :

3 - Si vous écrivez maintenant 2 (x + 6) = 4 x + 6, vous pouvez croire à première vue que c'est faux, et ce serait faux en effet, si vous aviez voulu écrire une identité. L'égalité ci-dessus, n'est vérifiée que pour une valeur particulière de x. C'est une équation. Si vous donnez la valeur 3 pour x, l'équation est résolue et vous avez retrouvé une égalité numérique. Aucune autre valeur de x ne résout cette équation.

Définition : Une équation est une égalité littérale qui n'est vérifiée que pour certaines valeurs attribuées aux lettres qu'elle contient.

Ces valeurs sont les solutions ou racines de l'équation.

Résoudre une équation c'est trouver toutes ces racines (ou solutions). Dans des équations complexes, plusieurs solutions peuvent répondre au problème et résoudre l'équation. Nous n'étudierons pas les équations dites du second ou troisième degré, ce qui sortirait du cadre de notre leçon, qui n'a pour but, comme nous l'avons dit, de vous faciliter la compréhension des différentes théories.

4. 2. - RÉSOLUTION DES ÉQUATIONS

Pour résoudre une équation, il faut essayer de la remplacer par une équation équivalente plus simple, dont on connaît les racines.

Règle 1 : Lorsqu'on ajoute ou retranche une même expression algébrique aux deux membres d'une équation, on obtient une équation équivalente à la première.

On peut ajouter (ou retrancher) aux deux membres, un nombre algébrique «A» quelconque sans modifier l'équation.

«A» peut être un nombre pur, ou contenir l'inconnue x.

Remarque : On peut transposer un terme d'un membre d'une équation dans l'autre à condition de changer son signe.

Exemple :

Retranchons 3 dans chaque membre :

Effectuons les opérations possibles dans le premier membre ; il reste :

Nous observons que le terme 3, qui avait le signe + dans le premier membre, a le signe moins dans le second, ce qui confirme bien la règle énoncée.

Appliquons donc cette règle pour le terme 3x :

---------------------------------------------------------» - x = 1

-------------------------------------------------------» ou x = - 1

Remarque : Il faut toujours, dans le résultat final, exprimer «x positif». Dans le cas où l'on obtient «x négatif», il suffit de multiplier les deux termes de l'équation par - 1 pour obtenir «x positif».

Règle 2 : Lorsqu'on multiplie ou divise les deux membres d'une équation par une même expression algébrique non nulle, on obtient une équation équivalente à la première.

   

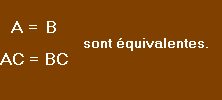
A, B et C étant des expressions algébriques.

APPLICATIONS :

1 - On peut «chasser les dénominateurs» d'une équation, en multipliant un de ses membres par le dénominateur de l'autre et inversement.

Exemple :

Pour «chasser» les dénominateurs, on multiplie par 15 le membre de gauche et par 4 le membre de droite :

Nota : Cela nous rappelle la propriété des proportions «produit des extrêmes = produit des moyens».

La solution est :

Autre exemple :

Multiplions par 4 le membre de droite. 4 «est chassé» du membre gauche et vient multiplier le membre droit.

La résolution de l'équation se poursuit, alors, comme nous l'avons vu ci-dessus :

2 - On peut simplifier une équation en divisant les deux membres par un même nombre non nul.

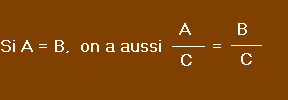
Avec C, non nul. (Autre propriété des proportions).

Remarque :

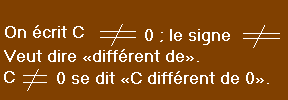
Exemple de calcul :

Nous avons l'équation suivante :

On remarque la présence de (x - 2) dans les deux membres. Nous pouvons donc les simplifier par x - 2 selon la règle 2. Mais cette expression (x - 2) s'annule pour x = 2. Les deux membres sont alors multipliés par 0 et l'équation est vérifiée. (On obtient 0 = 0).

Le nombre 2 est une première racine. Nous pouvons maintenant simplifier par (x - 2). Nous avons :

Nous avons donc trouvé à cette équation les deux racines :

Vous voyez d'après cet exemple, qu'il faut se garder de simplifier sans précaution, par une expression qui peut s'annuler : vous courrez le risque de supprimer une solution de l'équation.

Exemple de calcul :

1 - On «chasse» les dénominateurs :

2 - On effectue :

3 - On fait passer les inconnues à gauche et les valeurs numériques à droite.

On s'assure maintenant que la racine carrée trouvée n'annule pas un dénominateur :

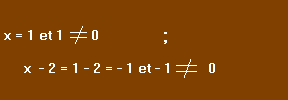
On peut donc confirmer que 1 est la racine de l'équation.

Remarque : La présence de 2x² indique une équation du second degré.

Dans ce cas, le terme en x² disparaît par le calcul, car il existe dans les deux membres. Nous revenons à une équation du 1er degré que nous savons résoudre. Si par contre après simplification, un terme en x² était resté présent, nous n'aurions pas pu résoudre l'équation n'ayant pas étudié les équations du second degré.

5. 2. - ÉQUATION A COEFFICIENTS LITTÉRAUX

Soit à résoudre : (ax - c) / b = (c - ax) / a

Cette équation n'a de sens que si les termes a, b et c sont différents de zéro.

1 - Chassons les dénominateurs :

2 - Passons les termes en (x) dans un membre, les termes sans (x) dans l'autre.

3 - Mettons (x) en facteur commun

Mettons maintenant «a» en facteur commun dans le premier membre :

4 - Pour obtenir x seul, il nous faut diviser le premier terme par a (a + b). Mais pour conserver l'égalité, divisons les deux membres par cette valeur :

 

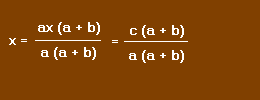
5 - Discussion :

Si a + b est différent de 0, nous pouvons simplifier par a + b et nous obtenons :

Si a + b est égal à 0, l'équation est de la forme :

Il est indéterminée. En effet, les deux membres sont toujours nuls quelle que soit la valeur que l'on donne à x.

Ces calculs peuvent vous paraître compliqués. Il n'en est rien. Ce ne sont que des applications de règles élémentaires que nous avons étudiées jusqu'à maintenant. Par contre, il est très important d'observer attentivement une équation avant de développer les calculs.

5. 3. - RÉSOLUTIONS D'ÉQUATIONS

5. 3. 1. - PAR LES PRODUITS DE FACTEURS

Il est évident que pour qu'un produit de facteurs soit nul, il faut et il suffit que l'un des facteurs soit nul.

Exemple :

D'où deux possibilités et les deux solutions :

5. 3. 2. - PAR MISE EN FACTEUR COMMUN

Soit l'équation :

Mettons x en facteur commun :

Pour qu'un produit de facteurs soit nul, il faut et il suffit que l'un des facteurs soit nul.

D'où les deux solutions :

5. 3. 3. - ÉQUATION CONTENANT L'INCONNU EN FACTEUR DANS LES DEUX MEMBRES

On aperçoit le terme (x + 3) dans les deux membres. Nous avons rencontré un tel problème tout à l'heure.

Si le terme (x + 3) est nul, l'équation est vérifiée. C'est donc la première solution.

Si (x + 3) n'est pas nul, on peut simplifier les deux membres par (x + 3) et on trouve :

En résumé les deux solutions sont :

Nous terminons ainsi l'étude élémentaire de l'algèbre.

1. 1. - NOTION DE PROGRESSION

1. 1. 1. - PROGRESSION ARITHMÉTIQUE

Définition : On appelle progression arithmétique, une suite de nombres tels que chacun d'eux est égal au précédent augmente ou diminue d'un nombre constant appelé raison.

Exemple :

Progression arithmétique croissante de raison + 2 :

Progression arithmétique décroissante de raison - 3 :

1. 1. 2. - PROGRESSION GÉOMÉTRIQUE

Définition : On appelle progression géométrique une suite de nombres tels que chacun d'eux est égal au précédent multiplié ou divisé par un nombre constant appelé raison.

Exemple :

Progression géométrique croissante de raison 2 :

Progression géométrique décroissante de raison 3 :

1. 2. - LOGARITHME D'UN NOMBRE

1. 2. 1. - LOGARITHME D'UN NOMBRE SUPÉRIEUR A 1

Prenons une progression géométrique croissante de raison 10 et dont le premier est égal à 1 :

Prenons maintenant une progression arithmétique de raison + 1 et dont le premier terme est égal à 0.

Écrivons ces deux progressions l'une sous l'autre :

Si nous prenons deux nombres d'une même colonne, nous dirons par définition que le nombre de la progression arithmétique est le logarithme du nombre de la progression géométrique.

Ainsi, nous dirons que 2 est le logarithme de 100.

On écrit : log pour logarithme

Le logarithme correspond donc à l'exposant de la puissance de base 10 ; 2 est le logarithme de 10² = 100 ; 3 celui de 10³ = 1 000 ; 5 celui de 10⁵ ...

Règle : Le logarithme d'une puissance de 10 supérieur à 1 est positif et égal à l'exposant de la puissance de 10.

Remarque : La raison de la progression géométrique étant 10, les logarithmes obtenus, sont dits décimaux ou à base 10 ou encore vulgaires.

1. 2. 2. - LOGARITHME D'UN NOMBRE COMPRIS ENTRE 0 ET 1

La même progression géométrique que celle définie plus haut, donne :

La même progression arithmétique que ci-dessus vers les nombres négatifs, donne :

Écrivons les deux progressions l'une en-dessous l'autre. Comme précédemment, le nombre de la progression arithmétique est le logarithme du nombre correspondant de la progression géométrique.

Ainsi : log 10^-5 = log (1 / 10⁵) = - 5 ....    et    log 10^-1 = log 1 / 10 = - 1

Règle : Le logarithme d'une puissance de 10 inférieure à 1 est négatif et égal à l'exposant de la puissance de 10.

Le même procédé a été utilisé pour déterminer les logarithmes des nombres décimaux et des tables de logarithmes ont été établies. Nous parlerons de ces tables un peu plus tard.

1. 2. 3. - TABLEAU RÉCAPITULATIF

Résumons ce qui vient d'être dit.

On retiendra que :

      Les nombres négatifs n'ont pas de logarithme ;

      Le logarithme de 1 est égal à zéro ;

      Les logarithmes des nombres plus grands que 1 sont positifs ;

      Les logarithmes des nombres supérieurs à 0 et inférieurs à 1 sont négatifs ;

      Seules les puissances de 10 ont pour logarithmes des nombres entiers.

Exemples : log 1 000 = 3  ;  log 0,001 = - 3

1. 3. - PROPRIÉTÉS DES LOGARITHMES

1. 3. 1. - LOGARITHMES D'UN PRODUIT

Soient deux nombres A et B, et a et b leurs logarithmes.

Nous pouvons écrire d'après la définition même des logarithmes (paragraphe 1. 2.)

Soit maintenant le produit AB :

et en prenant le logarithme des deux membres :

D'où la formule fondamentale suivante :

Vous voyez tout de suite l'intérêt des logarithmes : on a remplacé le calcul d'un produit par celui d'une somme.

En généralisant, nous écrirons :

Exemple : Nous devons calculer le logarithme du nombre 300.

Nous allons décomposer 300 en un produit de facteurs inférieurs à 100.

D'où, en appliquant les règles précédentes :

On aurait encore pu écrire :

Ou encore :

1. 3. 2. - LOGARITHME D'UN QUOTIENT

Soit le quotient A / B = Q

D'où l'on tire : A = B . Q

Appliquons la règle précédente :

Donc :

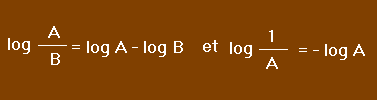
Une division a été remplacée par une soustraction.

Exemple :

Soit le quotient : 200 / 10 dont nous voulons connaître le logarithme.

Nous pouvons écrire :

Il est bien évident que nous aurions pu, au départ, calculer le quotient de 200 / 10, soit 20 et chercher le logarithme de 20 ou le calculer en fonction des règles connues et sachant que 20 = 2 x 10.

Autre exemple :

Soit le quotient 59 / 27 dont nous voulons connaître le logarithme :

La table ou tout simplement d'une calculatrice dite «scientifique» nous donne directement les valeurs :

1. 3. 3. - LOGARITHME D'UN NOMBRE ÉLEVÉ A UNE PUISSANCE P

Soit le nombre A élevé à la puissance p :

Exemple : Quel est le logarithme de 1 000 ?

Appliquons la dernière relation :

                                                                              log 10³ = 3

Autre exemple : Quel est le logarithme de 10^2,5 ?

                                                                           log 10^2,5 = 2,5

Troisième et dernier exemple :

Quel est le logarithme de 1 600 ?

Nous nous trouvons avec un produit dont chacun des termes est élevé au carré :

D'où :       log 1 600 = log 4² + log 10²

      log 4² = 2 log 4

           = 2 x 0,60206 = 1,20412

     log 10² = 2 log 1

 = 2 x 1 = 2

et enfin       log 1 600 = 1,20412 + 2

soit :     log 1 600 = 3,20412

1. 3. 4. - GÉNÉRALISATION

La formule ci-dessus reste valable si (p) est un nombre fractionnaire : p = m / n 

 

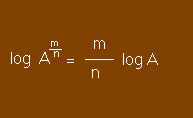
Or, une puissance fractionnaire est une extraction de racine.

 

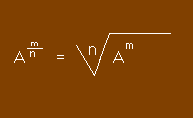
En particulier si m / n = 1 / 2, nous avons une extraction de racine carrée :

 

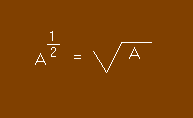
Vous sentez plus encore, dès maintenant, l'intérêt considérable que peuvent présenter les logarithmes. Une extraction quelconque de racine (aussi compliqué que l'on veut) qui serait inextricable par la méthode de calcul classique, se résout très rapidement à l'aide des logarithmes.

Prenons un exemple : Soit à extraire la racine carrée de 100.

 

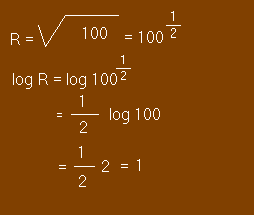
Or, le nombre R qui a pour logarithme 1 est 10, donc :

Nous voyons que les logarithmes permettent d'effectuer facilement des calculs complexes à condition, bien entendu, de bien connaître les règles d'application.

Sommaire