2.8. - PRODUIT LOGIQUE DE DEUX VARIABLES

2.8.1. - EXEMPLE ET DÉFINITION

Supposons maintenant que l'on demande : Jacques est-il à l'école ? OUI ou NON. Il y a de nouveau deux réponses possibles.

Mais maintenant, est-ce que Paul ET Jacques sont à l'école ?

Résumons les différentes réponses sur le tableau (figure 22).

Nous voyons que lorsque «Paul et Jacques sont à l'école» il faut «Jacques est à l'école» ET «Paul est à l'école.»

Nous venons de définir la fonction logique ET.

Nous pouvons écrire P = a . b que nous lirons P = a ET b.

2.8.2. - REPRÉSENTATION D'EULER OU DE VENN   (figure 23).

Si l'ensemble A est l'ensemble pour lequel la variable a = 1, et l'ensemble B celui pour lequel la variable b = 1, P est l'intersection de A et B, et représente le temps pendant lequel Jacques et Paul sont à l'école, c'est-à-dire l'ensemble des valeurs de P égales à 1.

2.8.3. - MONTAGE ÉLECTRIQUE   (figure 24)

Pour que la lampe s'allume, il faut appuyer sur a ET b simultanément. Jusque-là, nous avons dessiné les contacts (terme utilisé par les logiciens) ou interrupteurs (terme plus général) comme sur la figure 24 (représentation qui est très utilisée).

Étudions maintenant la représentation de la figure 25.

La logique positive fait correspondre à l'état physique contact fermé l'état logique 1, et à l'état physique contact ouvert l'état logique 0. L'interrupteur est toujours représenté au repos tombant de son propre poids : ce qui n'est pas nouveau.

Nous avons dit dans le chapitre traitant de l'information dans les systèmes numériques que le phénomène physique considéré est souvent une tension comme celle du signal numérique que nous avons décrit avec deux niveaux haut et bas bien déterminés.

Nous avons adopté les termes anglo-saxons High (H) qui signifie haut et Low (L) qui signifie bas car ils sont très souvent utilisés par de grands constructeurs de composants tel Texas ou dans certaines littératures. Nous utiliserons cette notation dans certains exemples afin de vous habituer dès maintenant à ces deux niveaux haut et bas.

Pour que la lampe S soit allumée, il faut a et b fermés c'est-à-dire au niveau haut d'où les tableaux de la figure 26.

2.8.4. - PROPRIÉTÉS DU PRODUIT LOGIQUE

Associons une variable binaire x avec 0 et 1, elle-même ou son complément.

Donnons une illustration de ces associations logiques au moyen de contacts électriques en utilisant la convention logique positive :

      1°)  x . 0 = 0  (figure 27)

Lorsque l'on appuie sur le bouton x, la variable passe à 1 mais le courant ne pourra jamais passer et S sera toujours éteinte d'où la table de vérité de la figure 27.

      2°)  x . 1 = x   (figure 28)

Lorsque l'on appuie sur le bouton x, la variable x agit seule sur le courant, en effet, le contact toujours à 1 n'a pas d'influence car il laisse toujours passer le courant d'où la table de vérité de la figure 28.

      3°)  x . x = x   (figure 29)

Lorsque l'on appuie sur les deux boutons x, la variable est à 1 et les deux contacts sont fermés de telle sorte que la lampe S s'allume. S prend la valeur de x d'où la table de vérité de la figure 29.

      4°)     (figure 30)

Lorsque l'on appuie sur le bouton, le contact x se ferme et le contact s'ouvre, la lampe n'étant ainsi jamais alimentée, donc toujours éteinte, d'où la table de vérité de la figure 30.

2.9. - SOMME LOGIQUE DE DEUX VARIABLES

2.9.1. - EXEMPLE ET DÉFINITION

Supposons maintenant que deux enfants du village, Paul et Jacques vont à l'école de la ville voisine. Quand y aura-t-il au moins un enfant du village dans le bus de ramassage scolaire qui les y conduit ?

Résumons les possibilités sur le tableau de la figure 31.

Nous voyons qu'il y a un enfant du village dans le bus lorsque Paul OU Jacques est dans le bus, mais pas seulement lorsque l'un ou l'autre est dedans, mais aussi lorsqu'ils y sont tous les deux.

C'est pourquoi nous disons que la fonction S = f (a,b) est un OU INCLUSIF (car elle inclue le cas où a et b sont présents en même temps).

En algèbre de Boole (par commodité typographique), on note l'opération OU inclusif +.

Exemple :

a + b = 1 qui s'énonce a OU b vaut 1.

Contrairement à l'algèbre traditionnel, le signe + ne signifie pas plus mais OU, en effet 1 + 1 = 1 en algèbre de Boole !

Nous avons vu précédemment ce qui est fondamental, que les valeurs prises en compte sont des états et non des nombres.

2.9.2. - REPRÉSENTATION D'EULER OU DE VENN   (figure 32)

Soit les variables logiques a et b. Dessinons dans le référentiel Â, la surface ou l'ensemble A à l'intérieur duquel la variable a est à 1 et l'ensemble B à l'intérieur duquel la variable b est à 1.

L'ensemble dans lequel les variables a ou b sont à 1, ou somme logique, sera la surface formée de la réunion des deux régions précédentes.

En algèbre de Boole, nous utiliserons uniquement la notation :

S = a + b  que l'on lit  S = a OU b

2.9.3. - MONTAGE ÉLECTRIQUE   (figure 33)

Nous voyons qu'il suffira de fermer a OU b pour que la lampe S s'allume (ou les deux à la fois).

On peut écrire S = a + b d'où la figure 34 :

2.9.4. - PROPRIÉTÉS DE LA SOMME LOGIQUE

Associons une variable binaire x avec 0 et 1, elle-même ou son complément.

Pour cela, nous allons donner une illustration de cette association logique au moyen de contacts électriques (convention logique positive).

      1°)  x + 0 = x   (figure 35).

Lorsque l'on appuie sur le bouton x, la variable x passe à 1 et le courant alimente la lampe S d'où la table de vérité de la figure 35.

      2°)  x + 1 = 1   (figure 36)

Lorsque l'on appuie sur le bouton x, la variable x passe à 1, mais ceci n'a pas d'effet car la lampe S reste allumée en permanence d'où la table de vérité de la figure 36.

      3°)  x + x = x   (figure 37)

Les deux contacts x sont liés mécaniquement, ils se ferment simultanément, nous pourrions remplacer la figure 37 par la figure 38 : les tableaux de vérité sont identiques pour S par rapport à x. Un des contacts x peut être supprimé.

Lorsque le courant ne passe pas par x il passe par et la lampe S est toujours alimentée, d'où la table de vérité de la figure 39.

2.10. - GÉNÉRALISATION DES PROPRIÉTÉS DES OPÉRATIONS LOGIQUES

Nous pouvons déduire des propriétés vues précédemment : le tableau récapitulatif (figure 40).

      1°)  Commutativité

On peut écrire que a + b = b + a ce qui est vérifié dans l'exemple du tableau (figure 40) : 0 + 1 = 1 et 1 + 0 = 1 mais aussi a . b = b . a ce qui se vérifie dans le même tableau (figure 40) : en effet 0 . 1 = 0 et 1 . 0 = 0.

      2°)  Idempotence

Pour la somme logique on peut écrire : a + a + a = a

Pour le produit logique on peut écrire : a . a . a = a

Cette propriété découle également du tableau de la figure 40.

      3.a)  Distributivité du produit logique par rapport à la somme logique

On peut facilement vérifier que :

a (b + c) = ab + ac

Cette propriété est appelée distributivité du produit logique par rapport à la somme logique ; elle est identique à la distributivité de la multiplication par rapport à l'addition dans l'algèbre traditionnelle.

      3.b)  Représentation d'Euler 

La figure 41 montre les 3 ensembles a, b, c.

Dessinons figure 42 l'ensemble S = a (b + c) intersection de a et de b + c.

Construisons maintenant figure 43, les ensembles ab et bc ainsi que leur réunion S = ab + ac. 

Nous voyons que la surface S est la même dans les deux cas.

      4.a)  Absorption

Considérons a + ab que l'on peut écrire a (1 + b), or nous savons que b + 1 = 1, d'où l'on déduit que a + ab = a (1 + b) = a . 1 = a.

On appelle la propriété a + ab = a propriété d'absorption.

     4.b)  Représentation d'Euler

Considérons les ensembles a et ab dans la représentation d'Euler de la figure 44.

Nous voyons facilement que l'ensemble a + ab n'est autre que a.

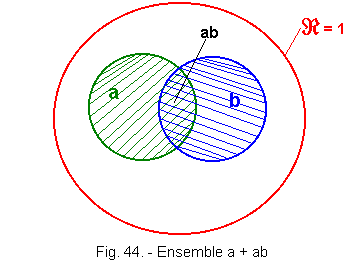
On peut dire que :

Lorsqu'une somme contient un terme et un de ses multiples, on peut négliger le multiple.

      5.a)  Somme d'une variable et d'un multiple de son complément.

Considérons S = a + b.

En utilisant le corollaire de la propriété d'absorption qui est parfaitement valable, on peut écrire :

S = a + b = (a + ab) + b = a + ab + b

d'où  S = a + b (a + )

or  a + = 1

d'où  S = a + b

a + b = a + b

On pourra dire que lorsqu'une somme logique est composée de la somme d'une variable et d'un multiple de son complément, on peut faire disparaître le complément.

      5.b)  Représentation d'Euler   (figure 45)

Nous voyons que b est la zone correspondant à : b (hachures bleu et rouge) et que a + b n'est autre que a + b.

      6.a)  Distributivité de la somme logique par rapport au produit logique.

Considérons S = a + bc

La propriété d'absorption permet d'écrire :

a = a + ab   ;   a = a + ac et comme a + a = a

On peut écrire a = a + ab + a + ac qui devient a = ab + ac + a

d'où  S = a + ab + ac + bc

Comme a = a . a

S =aa + ac + ab + bc

S = a (a + c) + b (a + c)

d'où  S = (a + b) (a + c)

a + bc = (a + b) (a + c)

      6.b)  Représentation d'Euler   (figure 46-a et 46-b)

On met facilement en évidence au moyen des cercles d'Euler figure 46 l'égalité (a + bc) = (a + b) (a + c).

2.11. - SYMBOLES D'USAGE GÉNÉRAUX (REPRÉSENTATION AMÉRICAINE)

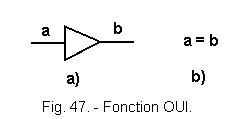
      1.)  Fonction OUI

Elle sera matérialisée par un fil électrique le plus souvent.

Elle pourra être matérialisée par le symbole du buffer (figure 47). Nous parlerons plus tard du buffer.

      2.)  Fonction NON   (figure 48)

Le symbole de la fonction NON est caractérisé par l'adjonction d'une bulle qui montre que la sortie de l'opérateur logique est inversée.

      3.)  Fonction ET   (figure 49)

      4.)  Fonction OU   (figure 50)

Il est à noter que ces symboles sont ceux d'opérateurs logiques contenus dans les circuits intégrés, par exemple, et bien qu'ils nécessitent une alimentation électrique, celle-ci n'est pas représentée.

Sommaire