6. - PROBLÈMES RÉSOLUS

6.1. - PROBLÈME N° 1

      Trois équipements : a, b, c, fonctionnent ensemble. Si, au moins deux de ces équipements tombent en panne, on désire alimenter automatiquement un élément de secours X.

• Le niveau logique «1» indiquera le bon fonctionnement,

• Le niveau logique «0» indiquera le mauvais fonctionnement.

      Donner la table de vérité,

      Tracer le tableau de Karnaugh,

      Après groupements, donner l'équation minimum,

      Dessiner le schéma logique,

      Réaliser ce schéma avec les circuits intégrés inverseurs, ET, OU... dont vous disposez (figure 76),

      Indiquer sur le schéma le brochage des circuits intégrés,

      Réaliser le même montage en utilisant que des fonctions NAND.

Vous disposez des trois circuits représentés figure 76.

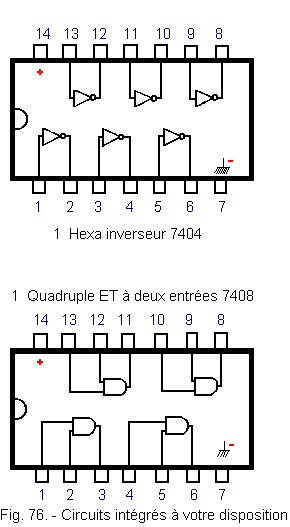
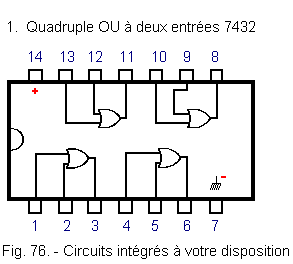
6.2. - SOLUTION DU PROBLÈME N° 1

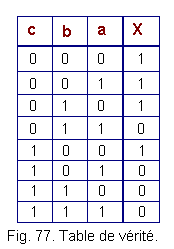
Nous voyons que X doit être à 1 chaque fois qu'au moins deux éléments sur a, b, c sont à 0 d'où la table de vérité de la figure 77.

Reportons dans le tableau de Karnaugh de la figure 78 les niveaux 1 de X pour les états correspondants de a, b et c.

D'après le tableau de Karnaugh, nous pouvons écrire :

• Groupement rouge =

• Groupement vert =

• Groupement bleu =

D'où l'on tire l'expression :

X = + +

On peut maintenant construire le schéma logique ou logigramme de la figure 79.

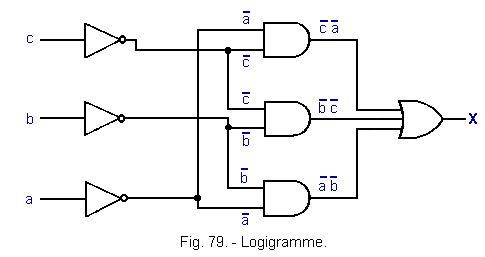
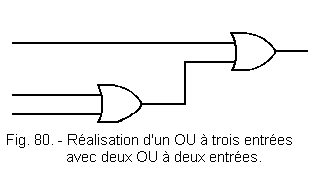
Nous voyons qu'en pratique un «OU» à trois entrées peut être remplacé par deux «OU» à deux entrées (figure 80).

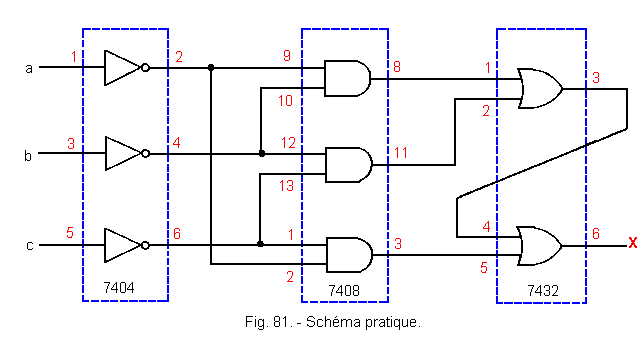
Le schéma devient alors celui de la figure 81.

Remplaçons chaque fonction logique par les équivalents à partir de NAND.

D'après le théorème de DE MORGAN, on peut remplacer un OU par trois NAND (figure 82).

En effet, = .

D'où S = a + b =

On peut donc transformer le schéma de la figure 83 de telle sorte qu'il devienne celui de la figure 84 et en supprimant les inverseurs inutiles celui de la figure 85.

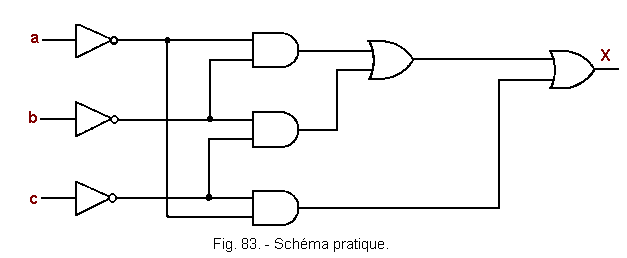
6.3. - PROBLÈME N° 2

Considérons le dispositif de la figure 86.

Fonctionnement :

      On dispose d'un bouton Marche / Arrêt  K,

      L'électro-aimant «M» ne peut être excité que lorsque le contact «d» = 1 (vanne fermée),

      «c» est alors libéré et devient «c» = 0,

      Le sable se déverse dans le dispositif de pesage B (a est alors à 1),

      Le ressort de pesage s'écrase, «a» passe à 0, mais «b» reste encore à 0 (état intermédiaire entre «a» et «b»),

      «b» = 1, ceci provoque la désexcitation de l'électro-aimant M,

      Le contact «c» repasse à 1,

      «c» excite alors l'électro-aimant N et donc «d» passe à 0,

      Le sable se déverse dans le wagonnet, «b» = 0, mais «a» reste encore à 0,

      «a» = 1, l'électro-aimant N est désexcité, la vanne se referme,

      Le contact d est alors actionné, «d» = 1 et le cycle recommence (M est excité, c est libéré...).

1°) - Donner la table de vérité du système pour les relais M et N,

2°) - Établir les tableaux de Karnaugh relatifs à M et N,

3°) - Logigrammes.

6.4. - SOLUTION DU PROBLÈME N° 2

6.4.1. - TABLE DE VÉRITÉ POUR LES SORTIES M ET N  (FIGURE 87)

Nous examinerons les combinaisons de variables dans l'ordre du déroulement du processus, nous ne tiendrons pas compte des combinaisons non utilisées.

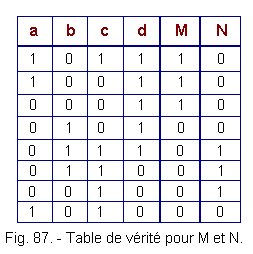
Les équations tirées de la table de vérité sont :

Équation de M

M = acd + ad + d

Équation de N

N = bcd + bc + c

Les fonctions M et N sont incomplètement définies (certaines combinaisons des variables ne sont pas utilisées), nous les considérons à 0 dans le tableau de Karnaugh.

6.4.2. - TABLEAU DE KARNAUGH POUR LA SORTIE M  (FIGURE 88)

On peut réaliser deux groupements :

Groupement rouge = d

Groupement vert = ad

L'équation simplifiée est donc M = ad + d

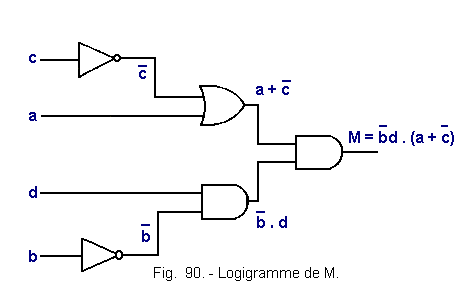
qui peut s'écrire : M = d (a + )

6.4.3. - TABLEAU DE KARNAUGH POUR LA SORTIE N  (FIGURE 89)

On peut réaliser deux groupements :

Groupement bleu = c

Groupement vert = bc

L'équation simplifiée est donc N = c + bc

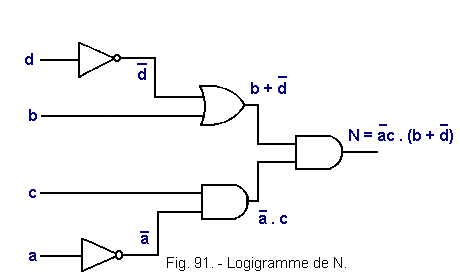
qui peut s'écrire : N = c (b + )

6.4.4. - LOGIGRAMME POUR M  (FIGURE 90).

6.4.5. - LOGIGRAMME POUR N  (FIGURE 91).

Sommaire