FORMULES MATHÉMATIQUES

NOTA : Dans ces leçons à pour but de représenter et de rassembler des formules, tables et graphiques utilisables dans les calculs élémentaires de géométrie, de physique et d'électronique.

Ils ont été conçus comme des aides mémoires de référence auxquels on pourra se reporter pour résoudre des problèmes relatifs au calcul des circuits. Il n'est donc pas nécessaire de se rappeler exactement les formules et les procédures de calcul des sujets exposés. Il suffira d'effectuer une seule fois les calculs indiqués dans les exemples pour se rappeler au moment opportun de l'existence d'une formule ou d'un graphique utilisable pour la solution d'un problème déterminé. En effet, même si l'on ne se rappelle que très vaguement d'une procédure, il sera toujours possible de recourir à ces leçons d'aides mémoires où sont indiqués les formules et graphiques qui permettront de résoudre les problèmes pratiques rencontrés dans le travail du technicien.

Toutefois, si vous désirez vous exercer à des calculs, vous pourrez faire à volonté de nouveaux exercices en les élaborant sur le modèle des exemples reportés dans ces leçons d'aides mémoires.

Dans ce but, il suffira de remplacer les valeurs numériques de l'exemple par d'autres valeurs choisies au hasard et d'effectuer les opérations avec les nouvelles données ; dans les cas plus complexes, vous pourrez vérifier l'exactitude du résultat final avec les preuves de calcul arithmétique.

Pour faciliter la lecture de ces leçons d'aides mémoires, les formules sont numérotées dans un ordre croissant, ainsi que les tables et graphiques.

Chaque formule est illustrée un exemple d'application pratique.

En général, on procède de la façon suivante : après avoir sélectionné la formule, on remplace les lettres du second membre par les valeurs numériques respectives (données) et l'on effectue les calculs pour obtenir le résultat final. Dans les cas plus complexes, il sera indiqué un contrôle supplémentaire qui pourra s'ajouter aux preuves du calcul arithmétique.

Parfois, il peut s'avérer avantageux de remplacer le calcul ordinaire, c'est-à-dire numérique, par une procédure particulière connue sous le nom de méthode graphique ; donc, outre le calcul ordinaire qui dérive directement de la formule, on pourra parfois prendre en considération également celui effectué par la méthode graphique.

Il peut arriver que l'on ait besoin de connaître les dimensions, surfaces ou volumes d'objets quelconques, et cela quand il n'est pas facile, ou même tout a fait impossible, d'effectuer des mesures directes. Il faut alors procéder à des calculs.

Par exemple, il peut se présenter des cas où il est nécessaire de connaître la longueur d'une spire, la section d'un conducteur, la section ou le volume d'un noyau magnétique...

En général, il s'agit de problèmes que l'on peut résoudre rapidement en appliquant une formule appropriée de géométrie.

Nous trouverons donc dans cette leçon d'aide mémoire les formules de géométrie ayant une application pratique en électronique.

FORMULE 1 - Calcul de la surface d'un triangle connaissant les valeurs de la base et de la hauteur (figure 1-a).

 

FORMULE 2 - Calcul de la surface d'un triangle équilatéral, "triangle ayant trois côtés égaux" (figure 1-b) connaissant la longueur du côté.

 

Exemple (figure 1-b) :

Surface : S 0,433 x 5² = 0,433 x 25 = 10,825 cm²

FORMULE 3 - Calcul de la surface d'un triangle isocèle "triangle ayant deux côtés égaux" connaissant la valeur des côtés égaux et de la base.

 

FORMULE 4 - Calcul de la surface d'un triangle scalène "triangle ayant trois côtés inégaux" connaissant la longueur des côtés.

 

Dans cette formule «p» désigne le demi-périmètre, c'est-à-dire la demi-somme des trois côtés. Avant d'appliquer la formule, il faut calculer à part la valeur «p» du demi-périmètre.

 

FORMULE 5 -  Calcul de l'hypoténuse d'un triangle rectangle connaissant les deux autres côtés (le triangle rectangle est un triangle ayant un angle de 90° ; l'hypoténuse est le plus grand côté, les deux autres côtés forment l'angle de 90°). (Voir la figure 1-e ci-dessus).

FORMULE 6 - Calcul d'un côté d'un triangle rectangle connaissant les longueurs de l'hypoténuse et de l'autre côté (pour la signification des termes, reportez-vous à la formule 5).

 

FORMULE 7 - Calcul de la surface d'un triangle rectangle connaissant les deux côtés de l'angle droit.

 

FORMULE 8 - Calcul de la diagonale d'un carré connaissant la longueur du côté. (Figure 2-a).

FORMULE 9 - Calcul de la surface d'un carré connaissant la longueur du côté.

Exemple (figure 2-a) :

FORMULE 10 - Calcul de la surface d'un carré connaissant la longueur de la diagonale.

Exemple (figure 2-a) :

Donnée : d 70,70 mm (valeur approchée établie avec la formule 8)

Surface : S 70,70² / 2 = 4 998, 49 / 2 = 2 499,245 mm²

Comparez ce résultat avec celui obtenu en appliquant la formule 9. La différence de 0,755 mm² (2 500 - 2 499,245 = 0,755) est due à l'introduction de la valeur approchée de 70,70 dans le calcul de la surface, mais l'erreur qui en résulte est très faible (seulement de 0,03 %), donc pratiquement négligeable.

(Pour faciliter la lecture, nous reportons la même figure ci-dessous à savoir figure 2).

FORMULE 11 - Calcul de la diagonale d'un rectangle connaissant les valeurs de la base et de la hauteur.

 

(Cette formule ci-dessus est similaire à la formule 5).

FORMULE 12 - Calcul de la surface d'un rectangle connaissant les valeurs de la base et de la hauteur.

Exemple (figure 2-b) :

FORMULE 13 - Calcul de la surface d'un losange connaissant la longueur des diagonales (le losange est un quadrilatère ayant quatre côtés égaux et des angles adjacents inégaux).

Exemple (figure 2-c) :

FORMULE 14 - Calcul de la surface d'un parallélogramme connaissant les valeurs de la base et de la hauteur.

(Cette formule ci-dessus est similaire à la formule 12).

Exemple (figure 2-d) :

FORMULE 15 - Calcul de la surface d'un trapèze connaissant les valeurs des deux bases et de la hauteur.

FORMULE 16 - Calcul de la surface d'un pentagone régulier connaissant la longueur des côtés (le pentagone régulier est un polygone ayant cinq côtés égaux et cinq angles égaux).

S 1,72 c² 

Exemple (figure 3-a) :

Surface : S 1,72 x 20² =  1,72 x 400 = 688 mm²

 

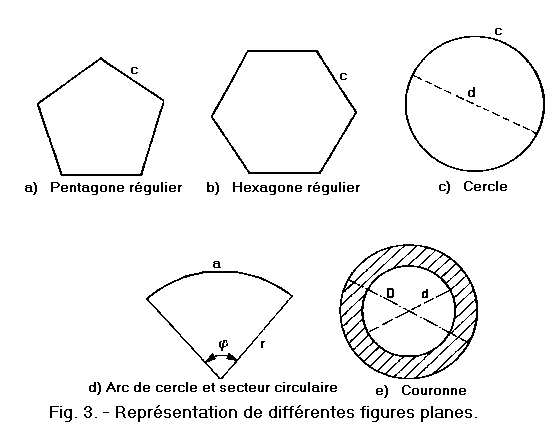
FORMULE 17 - Calcul de la surface d'un hexagone régulier connaissant la longueur d'un côté (l'hexagone régulier est un polygone ayant six côtés égaux et six angles internes égaux).

S = 2,60 x c²  

Exemple (figure 3-b "ci-dessus") :

Surface : S 2,60 x 12² = 2,60 x 144 = 374,4 mm² 

FORMULE 18 - Calcul du périmètre d'un cercle (circonférence) connaissant la valeur du diamètre.

 

FORMULE 19 - Calcul de la surface d'un cercle connaissant la valeur du diamètre. 

 

FORMULE 20 - Calcul de la longueur d'un arc de cercle connaissant la valeur de l'angle au centre et la longueur du rayon.

 

(Pour faciliter la lecture, nous reportons la même figure à savoir figure 3)

FORMULE 21 - Calcul de la surface d'un secteur circulaire connaissant la valeur de l'angle au centre et la longueur du rayon (un secteur circulaire est la surface plane délimitée par un arc de cercle et deux rayons).

 

FORMULE 22 - Calcul de la surface d'une couronne circulaire connaissant la valeur des deux diamètres (une couronne circulaire est la surface plane comprise entre deux circonférences concentriques).

 

FORMULE 23 - Calcul de la surface d'un segment de parabole connaissant la valeur de la base et de la hauteur (on appelle segment de parabole la surface plane comprise entre un arc de parabole et la corde sous-tendue entre les extrémités de l'arc).

Exemple (figure 4-a) :

 

FORMULE 24 - Calcul de la surface d'une ellipse connaissant la longueur des deux axes.

 

FORMULE 25 - Calcul de la longueur d'une hélice connaissant le nombre de spires, les valeurs du diamètre et de la hauteur.

 

FORMULE 26 - Calcul du volume d'un cube connaissant la longueur de l'arête.

Exemple (figure 5-a) :

 

FORMULE 27 - Calcul du volume d'un parallélépipède connaissant les valeurs de la longueur et de la largeur de la base, et la hauteur.

Exemple (figure 5-b) :

FORMULE 28 - Calcul du volume d'un cylindre connaissant les valeurs du diamètre et de la hauteur.

 

FORMULE 29 - Calcul du volume d'un cylindre creux connaissant les valeurs des deux diamètres et de la hauteur.

FORMULE 30 - Calcul du volume d'un anneau à section carrée connaissant les valeurs des diamètres externes et internes.

 

FORMULE 31 - Calcul du volume d'un tore (anneau à section circulaire) connaissant la valeur du diamètre extérieur et celle du diamètre de la section de l'anneau.

 

FORMULE 32 - Calcul de la surface d'une sphère connaissant la valeur du diamètre.

Exemple (figure 7-a) :

Surface : S 3,14 x 15² = 3,14 x 225 = 706,5 mm² 

 

FORMULE 33 - Calcul du volume d'une sphère connaissant la valeur du diamètre.

 

Exemple (figure 7-a) :

Volume : V 0,523 x 15³ = 0,523 x 3375 = 1765,125 mm³

FORMULE 34 - Calcul de la surface d'une calotte sphérique connaissant les valeurs du diamètre du contour et de la hauteur.

FORMULE 35 - Calcul du volume d'une calotte sphérique connaissant la valeur du diamètre de la base et de la hauteur.

 

FORMULE 36 - Calcul du volume d'une paraboloïde connaissant la valeur du diamètre de la base et de la hauteur.

 

Sommaire