LES CONDENSATEURS

Puisqu'il faut des quantités d'électricité différentes pour porter des corps de dimensions différentes à un même potentiel électrique, nous pouvons caractériser chaque corps par la quantité d'électricité qu'il doit posséder pour atteindre le potentiel de un volt ; cette quantité d'électricité est la capacité électrique (symbole C) du corps.

Pour un corps qui possède une quantité d'électricité déterminée, et qui se trouve à un potentiel déterminé, on obtient la capacité électrique en divisant la quantité d'électricité par le potentiel.

Par exemple, on obtient la capacité d'un corps qui a une quantité d'électricité de quatre coulombs et qui se trouve à un potentiel de huit volts en faisant la division 4 / 8 = 0,5 ; il faut donc 0,5 coulomb pour atteindre le potentiel de un volt, c'est-à-dire que la capacité électrique est de 0,5 coulomb par volt. Ainsi, la capacité électrique se mesure en coulomb par volt, unité de mesure à laquelle fut donné le nom de farad (symbole F), en l'honneur du savant Michaël FARADAY, déjà cité pour ses recherches sur les solutions électrolytiques. Le corps considéré dans notre exemple a donc une capacité de 0,5 farad.

Il faut noter qu'une sphère de la dimension de la terre aurait un capacité d'environ 1 F ; le farad est donc une unité de mesure beaucoup trop grande. Pour cette raison, en pratique, nous utilisons principalement les sous-multiples du farad soit :

      Le microfarad (symbole µF) qui équivaut à un millionième de farad (10^-6 F).

      Le nanofarad (symbole nF) qui équivaut à un milliardième de farad (10^-9 F soit 10^-3 µF).^-9 F soit 10^-3 µF).

      Le picofarad (symbole pF) qui équivaut à un millionième de millionième de farad (10^-12 F, soit 10^-6 µF ou 10^-3 nF).

La capacité d'un corps dépend en premier lieu de la présence dans son voisinage d'autres corps électrisés. Cette constatation peut être faite expérimentalement en considérant les deux plaques métalliques de la figure 1. 

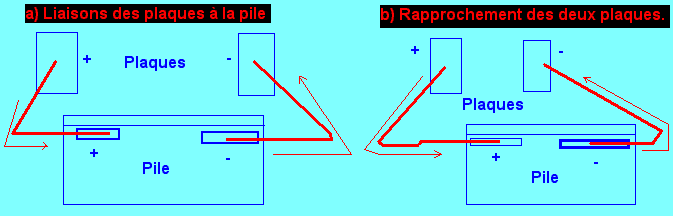
Ces deux plaques métalliques rigoureusement identiques sont reliées chacune à un pôle d'une pile, et se chargent d'électricité positive ou négative suivant le pôle auquel elles sont reliées.

A la figure 1-a, nous constatons que le processus de charge des deux plaques est très simple, un certain nombre d'électrons va du pôle négatif de la pile à la plaque qui lui est reliée, la chargeant négativement, tandis que le pôle positif de la pile attire un nombre égal d'électrons à la plaque qui lui est reliée ; celle-ci se charge positivement. Dans les conducteurs qui relient chaque plaque à la pile, il se crée un mouvement d'électrons dont le sens est indiqué figure 1-a. Le mouvement d'électrons cesse de lui-même lorsque la quantité d'électrons présente sur chaque plaque est telle que chaque plaque est au même potentiel que le pôle de la pile qui lui est relié. Entre les deux plaques existe la même différence de potentiel qu'aux bornes de la pile.

Comme nous l'avons vu précédemment, la quantité d'électricité que pourra emmagasiner chaque plaque dépend de sa capacité, or, les deux plaques étant identiques, elles possèdent la même capacité donc elles emmagasinent deux quantités d'électricité égales mais l'une est positive et l'autre négative.

Supposons à présent que nous rapprochons les deux plaques en les disposant bien en face l'une de l'autre, comme indiqué sur la figure 1-b, mais en évitant tout contact entre elles pour ne pas mettre la pile en court-circuit. De ce rapprochement des plaques, il apparaît une nouvelle circulation d'électrons, dans le sens indiqué figure 1-b et donc une augmentation de la quantité d'électricité contenu sur chaque plaque.

Pour le moment, limitons-nous à constater cet état de fait, l'explication en sera donnée plus tard.

Nous constatons que la quantité d'électricité sur chaque plaque a augmenté, bien que le potentiel de celles-ci n'ait pas changé. Nous pouvons donc affirmer qu'en rapprochant deux plaques, leur capacité augmente. Puisque la capacité change en faisant varier la distance entre les plaques, nous ne devons plus tenir compte d'une seule plaque mais considérer un ensemble constitué de deux plaques placées face à face à une distance déterminée, de la manière indiquée figure 2.

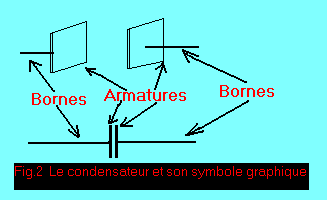
Cette disposition représente le type de condensateur le plus simple, qui est justement constitué de deux plaques en regard, appelées pour la circonstance armatures, munies de deux conducteurs (appelés bornes) pour leur raccordement aux circuits. A la figure 2 vous est également donné le symbole graphique du condensateur tel que vous le rencontrez dans les schémas électriques. Quelles que soient leurs caractéristiques ou le fabricant qui les conçoit, un condensateur est toujours constitué de deux armatures séparées par un isolant.

Pour définir la capacité d'un condensateur, il faut tenir compte de ses deux armatures et considérer ainsi la différence de potentiel existant entre elles.

Bien qu'un condensateur se compose dans tous les cas de deux armatures, une seule quantité d'électricité entre en ligne de compte. Elle est constituée des électrons qui, comme nous l'avons vu dans la figure 1, sont passés de l'armature devenue positive sur l'armature devenue négative et ceci par l'intermédiaire de la pile. Nous devons seulement considérer la quantité d'électrons manquante sur une armature ou bien celle présente en surplus sur l'autre, puisqu'il s'agit, en tout état de cause, de la même quantité d'électricité qui s'est transférée d'une armature sur l'autre.

La capacité d'un condensateur s'obtient en divisant la quantité d'électricité présente sur l'une de ses armatures par la différence de potentiel existant entre ses armatures.

Le condensateur est un élément des circuits électriques et se caractérise par sa capacité, comme la résistance est caractérisée par sa valeur résistive. Nous connaissons le rôle de la résistance qui est de produire des chutes de tension, et nous verrons ultérieurement le rôle du condensateur.

Le premier condensateur fut réalisé par le hollandais Pierre MUSSCHENBROCK (1692 - 1761) qui en découvrit les propriétés presque par hasard en même temps que l'allemand Georges VON KLEIST (1700 - 1748), au cours de ses expériences sur l'électricité.

Les expériences de ces savants ont montré l'influence qu'à sur la capacité d'un condensateur la matière isolante placée entre ses armatures, et qui constitue son diélectrique.

Le diélectrique du condensateur de la figure 2 est l'air et pour cette raison, ce condensateur est appelé condensateur à air.

Le diélectrique des condensateurs peut aussi être un autre matériau isolant tel que le mica, la papier paraffiné, le polystyrène, certaines substances céramiques, etc...

Très vite, les savants constatèrent que la capacité d'un condensateur à air augmentait quand ils mettaient entre ses armatures un diélectrique solide ; par exemple, une plaque de mica disposée entre les armatures d'un condensateur fait augmenter sa capacité de cinq à six fois, selon le mica employé. Ce qui signifie que, en ayant toujours la même différence de potentiel entre les armatures du condensateur, la quantité d'électricité présente sur celles-ci devient cinq à six fois supérieure si l'on remplace l'air par la feuille de mica. Ce comportement est dû au fait que le diélectrique solide mis entre les armatures du condensateur se polarise, comme nous allons le voir.

Considérons la figure 1-a sur laquelle est illustré un condensateur possédant un diélectrique solide. Le diélectrique occupe entièrement l'espace compris entre les deux armatures. Dans cette figure 1-a, apparaissent également quelques atomes du diélectrique, qui, pour simplifier notre explication sont supposés être constitués de quatre électrons gravitant autour du noyau sur une orbite unique.

Tant qu'aucune tension n'est appliquée aux bornes du condensateur, les électrons gravitent régulièrement autour de leur noyau respectif (fig.1 -a). Si par contre nous relions les armatures du condensateur aux bornes d'une pile comme dans la figure 1-b, les électrons sont attirés par l'armature qui devient positive et repoussée par celle devenant négative.

 

Comme le diélectrique est un isolant, les électrons ne peuvent pas quitter leur orbite, mais par contre, ils la modifient. Les électrons passent plus près de l'armature positive et plus loin de l'armature négative pendant la gravitation autour de leur noyau (figure 1-b).

Si nous considérons le phénomène dans son ensemble, nous voyons qu'il se crée un déplacement d'électrons qui, bien que demeurant liés à leur atome, se rapprochent néanmoins de l'extrémité gauche du diélectrique. Ce déplacement engendre ainsi une dissymétrie dans la distribution des charges électriques à l'intérieur du diélectrique.

L'extrémité gauche du diélectrique vers laquelle se dirigent les électrons devient négative et est appelée pôle négatif, tandis que l'extrémité droite qui voit s'éloigner les électrons est appelée pôle positif.

Nous pouvons dire que le diélectrique se polarise parce que ses extrémités prennent des polarités électriques différentes.

De la polarisation du diélectrique dépend de l'augmentation des charges présentes sur les armatures du condensateur et, en conséquence, cette polarisation détermine une augmentation de sa capacité.

Lorsque nous analyserons l'énergie relative à un condensateur, nous donnerons une explication sur ce fait. Pour le moment, il suffit de se rappeler que la capacité d'un condensateur dépend du matériau isolant dont est constitué son diélectrique, et plus particulièrement de sa polarisation inhérente à tel ou tel type de diélectrique.

Deux Condensateurs, dont les armatures sont de même surface et séparées par la même distance mais dont le diélectrique est différent, présentent des capacités différentes.

La différence entre les propriétés des matériaux constituant les diélectriques est caractérisée par la constante diélectrique absolue du matériau. Le symbole de la constante diélectrique absolue d'un matériau est E (lettre grecque et se lit «epsilon») ; son unité est le farad par mètre (symbole F / m).

Tout diélectrique possède sa propre constante diélectrique. Celle de l'air, qui est d'ailleurs considérée comme identique à celle du vide, est appelée constante diélectrique de l'air ou du vide et a pour symbole E₀ (epsilon zéro). E₀ vaut 1 / 36 pi X 10⁹ F / m soit pour faciliter les calculs : 8,85 pF/m. La connaissance de E₀ est très importante car en pratique, il n'est pas coutume d'indiquer la constante diélectrique absolue (E) d'un matériau et vous trouverez plutôt la constante diélectrique relative (Er) qui indique le rapport de la constante diélectrique absolue du matériau considéré et de la constante diélectrique de l'air ou du vide.

La constante diélectrique relative Er ne possède pas, quant à elle, d'unité (E₀ et E possédant la même unité qu'est le F / m).

A titre indicatif, sont reportées les valeurs de la constante diélectrique relative Er de quelques matériaux utilisés pour la réalisation du diélectrique des condensateurs

NOTE : La constante diélectrique relative est également appelée permittivité relative, de même que la constante diélectrique absolue est également appelée permittivité absolue.

Nous savons donc que la capacité d'un condensateur dépend de ses dimensions (surface des armatures et distance entre elles) et de son diélectrique : nous devons donc pouvoir calculer cette capacité d'après ces éléments, de même que nous avons pu déterminer la résistance d'un conducteur d'après ses dimensions et d'après la matière qui le constitue. 

Nous avons vu que lorsque nous augmentons la surface des armatures d'un condensateur, nous augmentons la quantité d'électricité présente sur celles-ci et donc aussi la capacité du condensateur : la capacité d'un condensateur est proportionnelle à la surface de ses armatures donc :

Nous avons vu ensuite que la quantité d'électricité sur les armatures augmente si nous diminuons la distance qui les sépare. Nous pouvons conclure que la capacité d'un condensateur est inversement proportionnelle à la distance qui sépare ses armatures :

Enfin intervient la constante diélectrique absolue du matériau utilisé. Plus cette constante est élevée, plus grande est la capacité du condensateur :

De la combinaison des trois relations que nous venons d'établir, la formule générale de calcul d'un condensateur devient donc :

C : Capacité en F

E : Constante diélectrique absolue en F / m

S : Surface des armatures en m²

d : Distance entre les armatures (ou épaisseur du diélectrique) en m

Toutefois, comme nous considérons le plus souvent la constante diélectrique relative, la formule précédente devient :

Après avoir examiné tous les éléments du condensateur qui influent sur sa capacité, nous allons analyser le comportement du condensateur lorsqu'il est inséré dans un circuit électrique de manière à comprendre les raisons pour lesquelles ce composant est très utilisé en pratique.

Examinons le circuit de la figure 3 dans lequel le condensateur est représenté par son symbole graphique.

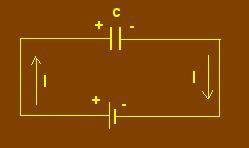
Dès que le condensateur (C) est relié à la pile, il se produit le phénomène déjà analysé précédemment, à savoir qu'un certain nombre de charges électriques passent d'une armature à l'autre. Ce déplacement constitue un courant électrique qui, sur la figure 3, est dirigé suivant le sens conventionnel. Ce courant est appelé courant de charge du condensateur.

Le courant de charge persiste jusqu'à ce que la quantité d'électricité parvenue sur les armatures du condensateur engendre, entre celles-ci, une différence de potentiel égale à la tension de la pile. Le condensateur est alors dit chargé.

Une fois le condensateur chargé, il ne circule aucun courant dans le circuit, étant donné que la tension créée aux bornes de (C) est égale mais opposée à la tension de la pile.

La décharge du condensateur peut facilement être observée. Il suffit de retirer le condensateur et de le brancher par exemple, aux bornes d'une résistance, comme illustré fig.4.

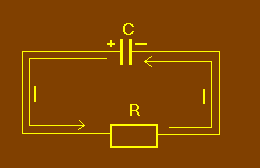
La tension présente aux bornes du condensateur fait circuler un courant dans la résistance R qui, selon le sens conventionnel, est dirigé de l'armature positive vers l'armature négative. Ce courant dû aux charges électriques accumulées sur les armatures du condensateur ne dure qu'un bref instant. Il cesse lorsque les charges présentes en surnombre sur une armature ont rejoint l'armature sur laquelle elles font défaut. Cette opération réalisée, le condensateur est dit déchargé et le courant créé par cette décharge est appelé courant de décharge du condensateur.

Si le condensateur une fois retiré de son circuit de charge (figure 3) n'est pas relié à une résistance, il conserve sur ses armatures les charges accumulées.

Le condensateur resterait chargé indéfiniment et le diélectrique se trouvant entre ses armatures était un isolant parfait. En pratique, cela n'arrive jamais et le diélectrique laisse passer petit à petit les charges électriques d'une armature à l'autre, ce qui décharge lentement le condensateur.

Le fait le plus important à retenir de ce que nous venons de voir est :

qu'un condensateur, après s'être chargé, empêche toute circulation ultérieure du courant fourni par une pile.

Nous venons de voir comment nous pouvons charger un condensateur au moyen d'une pile et le décharger ensuite dans une résistance. Il est facile de comprendre que lors de ces deux opérations, de l'énergie électrique est mise en jeu. Pour cela, il suffit d'observer l'effet thermique engendré dans la résistance par le courant de décharge du condensateur. Cet effet thermique se fait forcément au prix d'une consommation d'énergie électrique.

Cette énergie consommée a évidemment été fournie par le condensateur qui, lui-même, l'avait reçue de la pile. Si le condensateur est en mesure de céder cette énergie à la résistance, c'est qu'il ne l'a pas auparavant dissipée mais emmagasinée.

Le condensateur a la propriété d'emmagasiner l'énergie électrique, il est donc un élément conservateur d'énergie à la différence de la résistance qui est un élément dissipateur. Voyons maintenant comment il est possible de quantifier l'énergie électrique emmagasinée par un condensateur et de quelle manière celle-ci s'est emmagasinée.

Pour charger un condensateur, la pile doit déplacer une quantité d'électricité (Q) d'une armature à l'autre de ce composant. Cette quantité d'électricité est déterminée par le produit de la tension (V) de la pile par la capacité (C) du condensateur. Pour produire ce phénomène, une certaine énergie (W) est fournie par la pile et cette énergie est égale au produit de la quantité d'électricité (Q) par la tension (V).

Cependant, cette énergie (W) n'est pas emmagasinée totalement par le condensateur, en réalité, le condensateur n'emmagasine que la moitié de l'énergie (W) fournie par la pile. La seconde moitié est dissipée en chaleur dans la résistance interne de la pile et éventuellement dans d'autres résistances du circuit.

Pour s'en convaincre, examinons la figure 5 où la résistance (R) représente la résistance totale du circuit, c'est-à-dire la résistance interne de la pile plus celle des liaisons électriques et des armatures du condensateur.

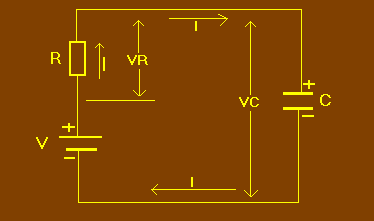
Au moment où le condensateur est relié au circuit, la tension Vc à ses bornes est nulle, donc toute la tension V de la pile se retrouve aux bornes de la résistance R (Vr = V). Puis au fur et à mesure de la charge du condensateur, la tension Vc augmente, tandis que Vr diminue. Quand la charge est terminée, toute la tension de la pile se retrouve aux bornes de C, tandis que Vr est nulle.

Les tensions Vc et Vr possèdent ainsi une allure analogue mais inverse puisque l'une est croissante et l'autre décroissante. Puisque le courant électrique (I) traverse à la fois R et C, la quantité d'électricité (Q) fournie par la pile au circuit se divise bien en deux parties égales entre R et C. L'énergie Wc emmagasinée par le condensateur est donc égale à l'énergie Wr dissipée dans la résistance.

L'énergie totale W fournie par la pile est égale à Wr + Wc mais comme Wr = Wc, nous avons également Wr = Wc / 2.

L'énergie fournit par une pile pour charger un condensateur est donnée par la formule W = Q x V ; ceci nous permet de quantifier l'énergie réellement emmagasinée par le condensateur :

Ou encore sachant que la quantité d'électricité accumulée par un condensateur est donnée par le produit Q = C x V, nous pouvons remplacer Q dans la formule précédente par sa valeur et nous obtenons :

Toute l'énergie Wc emmagasinée par le condensateur est ensuite intégralement restituée par celui-ci lors de sa décharge..

PARENTHÈSE : Il est intéressant de voir selon quelles lois varient la tension aux bornes du condensateur et le courant qui circule dans le circuit pendant la charge du condensateur. Ces allures sont reportées respectivement figure 6-b et 6-c tandis que la figure 6-a donne le circuit électrique pris comme exemple :

 

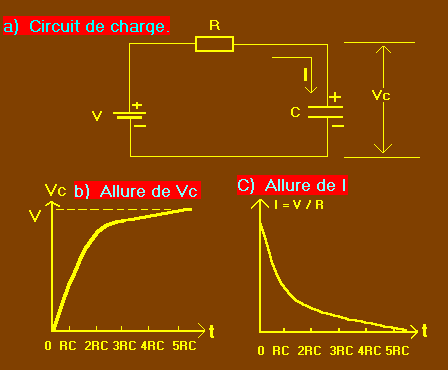
A l'instant initial t₀, où la liaison électrique est établie, il circule de la pile au condensateur un courant I = V / R égal à celui qui circulerait en permanence si nous avions non pas un condensateur mais un simple fil ne présentant aucune résistance (fig. 6-c). Juste après t₀, le condensateur commence sa charge et la tension Vc à ses bornes croît (fig. 6-b). En conséquence, le courant (I) commence à décroître jusqu'à s'annuler lorsque (C) est chargé : la tension aux bornes de (C) est maximale.

Les variations du courant et de la tension ont une allure dite exponentielle, les équations de telles courbes sont les suivantes :

équations dans lesquelles (e = 2,72 approximatif, représente la base des logarithmes naturels ou népériens et la valeur donnée par le produit RC (Résistance en ohm et capacité en farad) constitue la constante de temps du circuit mesurée en secondes. De ces lois découle que dans n'importe quel intervalle de temps égal à RC (de 0 à RC, de RC à 2 RC, etc...), la valeur du courant (de charge ou de décharge) diminue toujours dans un même rapport de 2,72.

Exemple : Prenons l'intervalle de 0 à RC, donc (t = RC)

Le courant (I) a bien diminué de 2,72 fois puisque à t = 0, sa valeur était de V / R et qu'au temps t = RC, sa valeur est de V / R / 2,72.

Il s'en suit que théoriquement le courant ne s'annule jamais et que le temps de charge ou de décharge du condensateur est infiniment grand. Toutefois, en pratique, nous constatons qu'après un temps égal à 5 fois la constante RC, le courant vaut 0,7 % de sa valeur initiale et nous pouvons considérer que la charge (ou la décharge) du condensateur est terminée.

Nous allons à présent analyser de quelle façon le condensateur emmagasine de l'énergie.

Supposons que nous chargeons un condensateur à air et imaginons qu'une des charges positives présentes en excédant sur l'armature positive se détache de celle-ci et se trouve dans le diélectrique (figure 7-a).

 

Cette charge est repoussée par l'armature positive alors qu'au contraire, elle est attirée par l'armature négative. Sur cette charge agit donc une force ayant la direction donnée par la flèche sur la figure 7-a. Cette même force agirait sur tout autre charge positive se détachant de l'armature positive.

Si nous traçons les parcours suivis par un certain nombre de charges, nous obtenons les différentes trajectoires représentées en traits fléchés (figure 7-b).

Ces lignes sont appelées lignes de force parce que la force qui détermine le déplacement des charges positives agit le long de celle-ci. L'ensemble des lignes de force délimite la zone de l'espace dans lequel une charge électrique est soumise à une force. La zone ainsi déterminée représente un champ de force électrique ou plus simplement un champ électrique.

Toute charge positive qui se trouve dans le champ est soumise à l'effet d'une force et tend à se déplacer. Cette force accomplit un travail qui est donné par le produit de l'intensité de la force par la longueur du déplacement de la charge. Tout travail s'obtient au prix d'une consommation d'énergie. Dans le cas du condensateur, l'énergie consommée pour produire le travail est l'énergie électrique emmagasinée par le condensateur.

Nous comprenons donc que l'énergie emmagasinée par le condensateur diminue à chaque fois qu'une charge se détache de l'armature positive et passe sur celle négative. A chaque transfert, une petite de l'énergie est transformée en travail accompli par la force qui engendre le déplacement de la charge. Si toutes les charges se détachent de leur armature, la totalité de l'énergie emmagasinée par le condensateur se transforme en travail et celui-ci se décharge complètement.

En réalité, aucune charge ne peut se détacher de l'armature positive étant donné que le diélectrique est un isolant presque parfait. Par contre, ces charges peuvent se déplacer en même temps que l'armature.

Analysons les conséquences d'un rapprochement des deux armatures, conséquences que nous connaissons mais auxquelles aucune réponse précise n'a été apportée.

Nous supposons que le condensateur de la figure 8-a possède une capacité de 3 µF et qu'il est chargé par une pile de 4 volts. La quantité d'électricité (Q) présente sur ses armatures est donné par la formule Q = C x V soit 3 µF x 4 V = 12 µC.

Si maintenant le condensateur est débranché de la pile, il conserve évidemment la quantité d'électricité de 12 µC et une tension entre ses armatures de 4 V.

Imaginons que l'armature positive se rapproche de l'armature négative et que la distance entre elles soit réduite de moitié (figure 8-b).

Si l'armature positive vient en contact avec l'armature négative, autrement dit si elle se déplace d'une distance d, toute l'énergie emmagasinée par le condensateur se transforme en travail. Nous comprenons donc que si l'armature positive se déplace de d/2, l'énergie emmagasinée est réduite de moitié. Toutefois, comme les deux armatures sont isolées, la quantité d'électricité ne peut pas diminuer ; en conséquence, c'est la tension entre armatures qui est réduite de moitié et prend pour valeur 2 volts (figure 8-b). La valeur du condensateur augmente et devient :

Nous venons ainsi d'apporter une explication concrète au fait que la capacité d'un condensateur augmente quand la distance entre ses armatures diminue et que, en particulier, elle double quand la distance est réduite de moitié.

Au début de cette leçon, nous avions rapproché les armatures tout en laissant le condensateur branché à la pile (figure 1) et nous avions vu que la pile fournissait un courant de charge supplémentaire. Nous pouvons dire maintenant que ce courant sert à conserver la tension aux bornes du condensateur égale à la tension fournie par la pile.

Introduisons à présent entre les armatures du condensateur chargé de la figure 8-a, mais non relié à la pile, un diélectrique solide (figure 8-c). Si ce diélectrique a une constante diélectrique relative Er de 2, la capacité du condensateur est doublée. L'introduction de ce diélectrique place le condensateur dans les mêmes conditions que dans la figure 8-b, après un rapprochement de ses armatures.

Dans ce cas également, la moitié de l'énergie emmagasinée est transformée en travail, mais puisqu'il n'y a pas déplacement d'armatures, ce travail est forcément produit différemment. Pour expliquer cela, il faut se souvenir du principe de polarisation du diélectrique exposé figure 1-a et 1-b (polarisation du diélectrique). L'excentration des orbites électroniques est déterminée par l'intensité du champ qui tend à attirer les électrons vers l'armature positive du condensateur. Le travail accompli par cette force sur chaque électron est très faible, cependant le nombre des électrons du diélectrique étant considérable, la somme des différentes forces aboutit à la consommation de la moitié de l'énergie emmagasinée par le condensateur.

Nous savons maintenant que le champ électrique se caractérise par des lignes de force dont nous connaissons déjà la direction et le sens de leur action (figure 7-b), mais pour être complet sur le champ électrique, il faut aussi connaître son intensité.

L'intensité du champ électrique agissant dans le diélectrique d'un condensateur s'obtient en divisant la tension existant entre ses armatures par la distance qui les sépare.

Note : Ne pas confondre ce symbole avec celui de la force électromotrice d'une pile (f.e.m.) d'où la présence de la flèche sur le symbole indiquant qu'il s'agit d'un vecteur.

L'unité de l'intensité du champ électrique est le volt par mètre (symbole V / m).

Il est facile de comprendre que l'intensité du champ électrique augmente lorsque la tension entre les armatures augmente ou quand la distance qui les sépare diminue. Ce fait entraîne une conséquence de première importance pratique. Toutefois, l'intensité du champ électrique ne peut pas augmenter indéfiniment et, arrivée à un certain seuil, la valeur de l'intensité devient telle que les charges électriques peuvent traverser le diélectrique d'une armature à l'autre.

Ce passage de courant se manifeste sous la forme d'une violente décharge électrique, une sorte d'éclair qui perfore le diélectrique et établit un contact irréversible entre les armatures du condensateur. Le condensateur est alors dit en court-circuit et devient inutilisable. Nous pouvons considérer cette décharge du condensateur ou claquage comme une transformation instantanée en chaleur de toute l'énergie emmagasinée par celui-ci.

La valeur de l'intensité du champ pour laquelle il y a claquage est la rigidité diélectrique du matériau constituant l'isolant. Cette valeur est différente pour chaque type de matériau.

Chaque matériau diélectrique est donc caractérisé non seulement par sa constante diélectrique relative mais également par sa rigidité diélectrique.

Le tableau de la figure 9 donne la rigidité diélectrique des matériaux déjà énumérés dans la figure 1.1 pour leur constante diélectrique relative.

Pour les matériaux diélectriques couramment utilisés, la valeur de la rigidité diélectrique est extrêmement élevée et pour cela, nous utilisons comme unité non pas le V / cm mais le kV / cm comme dans la figure 9.

Par exemple, pour un condensateur dont les deux armatures sont distantes de 1cm et ayant du polystyrène comme diélectrique, le claquage se produit pour une tension de l'ordre de 400 kV.

Si la distance entre les armatures n'est que de 1 mm, le même claquage se produit à 40 kV. Il existe des condensateurs où l'épaisseur du diélectrique n'est que de quelques millièmes de millimètre et nous comprenons donc que leur claquage se produit même pour des tensions basses, tensions que nous rencontrons dans les circuits électriques ou électroniques où les condensateurs sont utilisés. Pour cette raison, chaque condensateur porte une indication de tension appelée tension de service : valeur qu'il ne faut pas dépasser sous peine d'endommager le composant suite à un claquage.

Rappelez-vous, à ce sujet : qu'un condensateur est caractérisé non seulement par sa capacité mais aussi par sa tension de service.

Même l'air peut perdre ses propriétés diélectriques suite à un claquage, ainsi vous notez que l'air possède une rigidité diélectrique qui est de 21 kV / cm pour l'air sec.

Les éclairs que nous observons lors des orages sont la manifestation du claquage de l'air. En effet, des charges électriques s'accumulent dans les nuages qui se comportent alors comme les armatures d'un condensateur.

Il s'établit ainsi un champ électrique entre deux nuages qui se trouvent à des potentiels différents ou entre un nuage et la terre. Lorsque l'intensité du champ électrique dépasse la rigidité de l'air, qui de surcroît diminue fortement lorsque l'air est humide, il se produit une décharge électrique entre les nuages ou entre la terre et le nuage.

Le deuxième cas est très dangereux et pour éviter que la décharge électrique ne produise des dégâts sur les habitations mettant en danger la vie de ses occupants, les édifices sont protégés par un paratonnerre.

Le paratonnerre étant l'endroit le plus élevé de l'édifice, il s'expose ainsi à la décharge électrique. Le paratonnerre, relié à la terre, lui transmet la décharge électrique. Pour faciliter le contact avec la terre, il faut noter la présence d'une plaque de fer enterrée dans le sol (obligatoire).

Nous n'avons, pour l'instant, considéré des circuits ne possédant qu'un seul condensateur, mais ces composants comme les résistances peuvent former différents groupements.

La figure 10 représente un groupement parallèle de deux condensateurs appelés pour la circonstance C₁ et C₂.

C₁ et C₂ possèdent chacun une armature reliée au pôle positif de la pile et l'autre armature reliée au pôle négatif de la même pile, si bien qu'aux bornes de chaque condensateur, il existe la même tension.

Cette dernière caractéristique est commune à tout groupement parallèle comme cela a déjà été dit lors de l'analyse des groupements de résistances.

Puisque entre les armatures de C₁ et C₂ nous appliquons la même tension, chaque condensateur se charge avec une quantité d'électricité d'autant plus grande que sa capacité est élevée.

Voyons de quelle façon nous pouvons déterminer la capacité équivalente (Ceq) présentée par un tel circuit, et ceci connaissant la valeur de C₁ et de C₂.

Dans ce but, imaginons de rapprocher les deux condensateurs jusqu'à mettre en contact leur armature reliée au même pôle, comme illustré figure 11-a. Cela est possible dans la mesure où les armatures sont reliées au même potentiel électrique.

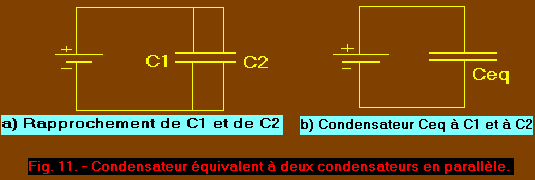
Les deux condensateurs ainsi réunis constituent un condensateur unique appelé Ceq dans la figure 11-b. Ce condensateur possède le même diélectrique, la même distance entre armatures que C₁ et C₂. La seule différence réside dans l'augmentation de la surface des armatures.

Compte-tenu de la formule donnant la capacité d'un condensateur :

Nous savons que si la surface S augmente, la capacité C du condensateur augmente également et ceci dans les mêmes proportions.

Dans le cas de la figure 11-a, la surface S de Ceq est égale à la somme des surfaces de C₁ et de C₂. Nous déduisons donc que la capacité du condensateur équivalent Ceq de la figure 11-b est égale à la somme des capacités de C₁ et de C₂.

La capacité équivalente à deux ou plusieurs condensateurs reliés en parallèle est égale à la somme des capacités de chaque condensateur :

Considérons les condensateurs C1 et C2 de la figure 12. Pour faciliter nos explications, les armatures de ces condensateurs sont appelées A, B, C et D.

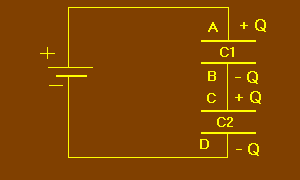
Lors de la charge de C1 et de C2, l'armature A se charge positivement et l'armature D négativement.

Les armatures B et C non reliées à la pile constituent avec le conducteur qui les relie, un simple corps métallique. Ce corps se charge par induction avec les signes représentés figure 12. Sur l'armature B apparaît un quantité d'électricité égale mais de signe opposé à celle présente sur A, tandis que sur C apparaît une quantité d'électricité égale mais de signe opposé à celle présente sur D.

Si nous appelons (+ Q) la quantité d'électricité présente sur A, nous avons (- Q) sur B, et si nous appelons (- Q) la quantité d'électricité présente sur D, nous avons + Q sur C.

Les condensateurs C1 et C2 emmagasinent donc la même quantité d'électricité Q.

Comme dans tout montage série, la tension V fournie par la pile se divise en deux tensions V1 et V2 respectivement aux bornes des condensateurs C1 et C2. Dans la figure 13 est reporté le même circuit avec les différentes tensions présentes.

La tension V1 aux bornes de C1 est égale à :

La tension V2 aux bornes de C2 est égale à :

Comme il est dit précédemment V = V1 + V2, donc :

 

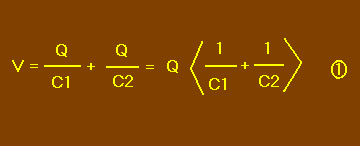
Nous pouvons remplacer dans la figure 13 les condensateurs C1 et C2 par un condensateur équivalent que nous appelons un Ceq (figure 14).

(Ceq) équivalent à C1 et à C2, emmagasine la même quantité d'électricité Q que C1 et C2.

Nous pouvons écrire la relation (2) :

En effet : Ceq = Q / V -----------» V = Q / Ceq = Q x 1 / Ceq

Les relations (1) et (2) sont égales puisqu'elles donnent toutes deux la valeur de la tension V.

En simplifiant (1) et (2) par Q, nous obtenons la valeur de Ceq :

Nous avons ainsi déterminé la valeur de Ceq en fonction de C1 et de C2. Étendue au cas général de plusieurs condensateurs en série, cette formule devient :

Ainsi, pour calculer la capacité équivalente (Ceq) de deux ou plusieurs condensateurs en série, les trois opérations suivantes sont à effectuer :

• Calculez l'inverse de chaque condensateur ;
• Additionnez les inverses ;
• Prendre l'inverse de la somme obtenue.

Quand deux condensateurs seulement sont en série, nous adoptons la formule suivante qui dérive de la formule générale :

Par un exemple pratique chiffré, mettons en application ce que nous venons de voir. Soit à calculer la capacité équivalente au circuit représenté figure 15.

Pour calculer Ceq, effectuons les trois opérations requises :

• Calcul de l'inverse de chaque condensateur :

• Somme des inverses :

• Prenons l'inverse du résultat :

Les condensateurs C1, C2 et C3 en série sont donc équivalents à une capacité unique de 1,25 nF.

Pour effectuer une comparaison entre les deux types d'associations, il faut noter que dans le cas de condensateurs en parallèle, la valeur du condensateur équivalent est toujours supérieure à la valeur de chaque condensateur tandis que dans le cas d'une association en série, la valeur du condensateur équivalent est dans tous les cas, inférieure à la valeur de chaque condensateur et même mieux, elle est inférieure à la plus petite des capacités.

Les formules présentées servent également aux calculs de circuits plus complexes nés de la combinaison des deux types d'associations.

Voyons par exemple, comment calculer la capacité totale du circuit représenté figure 16.

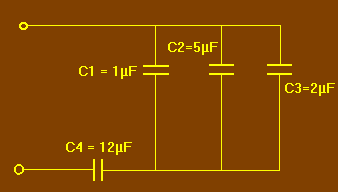
Dans ce circuit, nous voyons que C1, C2 et C3 constituent un groupement parallèle relié en série avec C4.

Calculons en premier lieu, le condensateur équivalent à C1, C2 et C3 en parallèle, condensateur que nous appelons C123.

Remplaçons dans la figure 16, C1 C2 et C3 par leur condensateur équivalent C123, nous obtenons la figure 17-a).

Avec la figure 17-a, nous sommes en présence de deux condensateurs (C123 et C4) reliés en série. Le calcul du condensateur équivalent (Ceq) à cet assemblage donne le condensateur équivalent au circuit de la figure 16 :

En présence de circuits complexes comme celui de la figure 16, il faut toujours simplifier le circuit progressivement jusqu'à n'obtenir plus qu'un seul condensateur dont la capacité représente la capacité globale du circuit de départ.

Ainsi se termine l'analyse des groupements de condensateurs.

Comme nous l'avons dit, il est important de savoir qu'un condensateur une fois chargé empêche toute circulation de courant fourni par une pile.

Dans les prochaines leçons, nous verrons qu'il existe d'autres générateurs fournissant des courants différents de celui fourni par une pile. Vis-à-vis de ces courants, les condensateurs réagissent différemment. Cette propriété est utilisée lorsque nous désirons séparer, dans un même circuit, deux types de courants différents.

Cette propriété sera analysée dans le détail lors des prochaines leçons suivantes.

Nous terminons cette leçon avec un tableau récapitulatif des grandeurs électriques relatives au condensateur ainsi que leur unité et leur formule si nécessaire (figure 18).

Dans la prochaine leçon, nous examinerons le troisième composant fondamental des circuits électroniques : l'inductance, ainsi que tous les phénomènes qu'elle engendre lorsqu'elle est introduite dans un circuit, par exemple l'électromagnétisme.

Sommaire