LIAISONS SÉRIE - LIAISONS PARALLÈLE
Dans les circuits électriques, les éléments qui
les constituent peuvent être reliés entre eux de
manières différentes selon les nécessités
; nous allons examiner les différents types de liaisons et
leurs propriétés particulières, qu'il s'agisse
des résistances ou des piles.
Revenons un instant à l'examen du circuit de la figure 1. Dans celui-ci, le courant I sortant de la borne "+" de la pile, traverse la résistance R totale et revient dans la pile par sa borne "-" et, pour distinguer ces deux résistances, nous les appellerons R1 et R2.

Le courant I fourni par la pile doit traverser successivement R1 puis R2 pour pouvoir revenir à la borne "-" de la pile.
Quand deux ou plusieurs éléments d'un circuit (dans ce cas deux résistances) sont traversés successivement par le même courant, on dit qu'ils sont reliés en série, ou plus simplement qu'ils sont en série. Le fait que le courant circulant dans ces éléments soit le même pour tous est une caractéristique spécifique des liaisons en série, donc plusieurs résistances en série sont toutes traversées par le même courant. (Ceci est évident et facile à comprendre).
L'adjonction de la résistance R2 rend la valeur résistive totale du circuit plus grande que s'il n'y avait que la résistance R1, car le courant, outre l'obstacle causé par R1 à son passage, doit également traverser R2. Nous pouvons dire que la résistance totale du circuit de la figure 1 ci-dessus qui s'oppose au passage du courant est donnée par la somme des valeurs résistives de chaque résistance. Rappelez-vous que :
La résistance équivalente présentée par plusieurs résistances reliées en série s'obtient en additionnant la valeur résistive de chacune des résistances.
Regardons maintenant ce qu'il advient de la tension délivrée par la pile. Aux bornes de chaque résistance, il apparaît une tension et ceci conformément à la loi d'Ohm.
Pour la figure 1, La tension V de la pile se partage entre les deux résistances R1 et R2 présentes dans le circuit. Aux bornes de R1 apparaît une tension V1 (déterminée par les valeurs de I et de R1) et aux bornes de R2 apparaît une tension V2 (déterminée par les valeurs de I et de R2). La somme de ces deux tensions est égale à la tension totale de la pile : V1 + V2 = V.
Illustrons par un exemple ce qui vient d'être affirmé.
Figure 2 est reporté le même circuit mais certaines grandeurs électriques sont agrémentées d'une valeur.

Dans ce circuit, nous devons déterminer l'intensité du courant I qui circule dans les résistances R1 et R2, ainsi que les tensions V1 et V2 présentent à leur bornes.
Les deux résistances étant reliées en série, toutes deux sont traversées par le même courant, donc la résistance globale offerte à la circulation de ce courant est déterminée par la somme des deux résistances soit :
L'application de la loi d'Ohm sous forme I = V / R nous permet de calculer I :
100 mA est l'intensité du courant qui traverse R1 et R2. Pour calculer les tensions V1 et V2 présentes aux bornes de R1 et de R2, la loi d'Ohm sera appliquée sous forme V = RI.
Ces résultats trouvés, nous constatons d'emblée que la tension V de la pile s'est partagée en deux parties et nous avons réalisé un circuit appelé diviseur de tension.
Dans les circuits électroniques, on a souvent recours à l'association de deux résistances en série dans le but d'obtenir une tension plus faible que celle fournie par l'alimentation du circuit.
Par exemple, supposons devoir alimenter une lampe fonctionnant sous 6 V et absorbant un courant maximum de 0,05 A (50 mA) à partir d'une pile de 9 V.
Sous peine de détruire la lampe, il est impossible de relier celle-ci directement à la pile étant donné que la tension trop importante de celle-ci ferait circuler un courant trop intense dans la lampe, courant qui "grillerait" (comme on dit couramment) la lampe.
Pour éviter cet inconvénient, nous pouvons disposer dans le circuit une résistance chutrice en série avec la lampe, comme illustré figure 3. Sur cette figure, vous ferez également connaissance avec le symbole graphique d'une lampe.

La valeur de la résistance R doit être calculée de façon adéquate pour qu'à ses bornes, la tension soit de 3 V (excédent fourni par la pile). Cette valeur peut être calculée par la loi d'Ohm car le courant I qui circule dans le circuit est imposé par la lampe L soit 50 mA et la tension VR à ses bornes de 3 V.
Remplaçons VR par V - VL (VL : tension aux bornes de la lampe L).
Dans ce cas, la résistance R reliée en série avec la lampe L forme avec celle-ci un diviseur de tension qui réduit la tension appliquée à la lampe, de manière à permettre son allumage dans de bonnes conditions.
On dit que la résistance R a ainsi "chuté" une partie de la tension fournie par la pile. Les résistances sont largement utilisées dans les circuits pour produire des chutes de tension, et réaliser ainsi des diviseurs de tensions.
Il y a un deuxième type de liaison utilisé pour les résistances est l'association en parallèle, illustrée figure 4.
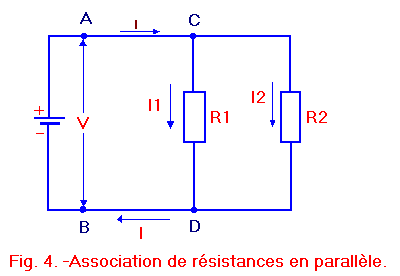
Dans ce type de montage, chacune des deux résistances R1 et R2 ont une de leurs bornes reliées au "+" de la pile et l'autre au "-". Toutes deux se voient donc appliquer la même tension, celle fournie par la pile. Cet état de fait est une caractéristique spécifique des liaisons en parallèle ; rappelez-vous que :
Aux bornes de plusieurs éléments associés en parallèle, il y a toujours la même tension.
Dans ce type de liaison, il faut donc essentiellement analyser le comportement du courant. Figure 4, notons pour le courant (I) qui sort du pôle positif de la pile se partage au point C en deux courants appelés I1 et I2 ; chacun de ses courants traverse une résistance (I1 traverse R1 et I2 traverse R2) puis se réunissent au point D pour reformer le courant initial (I) qui rejoint alors le pôle négatif de la pile.
Le courant I fourni par la pile est donc égal à la somme des courants qui traversent chacune des résistances.
Pour déterminer la résistance équivalente (Req) d'un tel assemblage, il nous faut utiliser la loi d'Ohm. La figure 5 est reporté le circuit électrique de la figure 4 ainsi que le schéma équivalent dans lequel apparaît Req.

Figure 5-a, nous pouvons déterminer la valeur du courant I en fonction de R1 et de R2.
Nous savons que dans un tel montage, la tension aux bornes de chaque résistance est égale à la tension fournie par la pile :
De la figure 5-b, nous déduisons que : (2) I = V / Req
Les deux égalités (1) et (2) donnent le même courant I et sont donc égales :
(1) = (2) ----------------------) V / R1 + V / R2 = V / Req
Multiplions les deux termes de l'égalité par 1 / V :
Simplifions les deux termes de l'égalité.
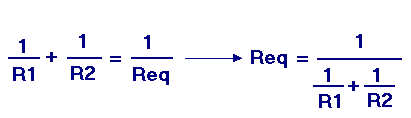
Nous avons ainsi déterminé la Req en fonction de R1 et de R2. Étendue au cas général de plusieurs résistances en parallèle, cette formule devient :

Lors de notre démonstration, nous sommes passés par le résultat intermédiaire suivant :
Autrement dit, l'inverse de la résistance équivalente est égale à la somme des inverses des résistances du circuit, ou pour être plus précis que la conductance équivalente est égale à la somme des conductances de chaque résistance.
Ainsi, pour calculer la résistance équivalente Req de deux ou plusieurs résistances en parallèle, on peut faire les trois opérations suivantes :
Quand deux résistances seulement sont en parallèle, on adopte la formule suivante qui dérive de la formule générale :
Par un exemple pratique chiffré, mettons en application ce que nous venons de voir :
Soit à calculer la résistance équivalente au circuit représenté figure 6.
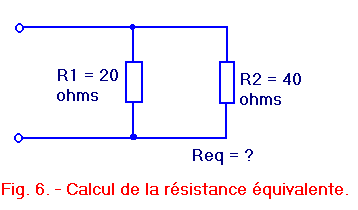
Pour calculer Req, effectuons les trois opérations requises :
Les résistances R1 et R2 en parallèle sont donc équivalentes à une résistance unique de 13,3 Ohms environ.
Pour comparer les deux types d'associations des résistances, nous pouvons noter que dans le cas de résistances en série, la valeur de la résistance équivalente est toujours supérieure à la valeur de chaque résistance tandis que dans le cas d'une association parallèle la valeur de la résistance équivalente est dans tous les cas inférieure à la valeur de chaque résistance et même mieux, elle est inférieure à la plus petite des résistances.
Les formules présentées servent également aux calculs de circuits plus complexes nés de la combinaison des deux types d'associations.
Prenons pour exemple le circuit de la figure 7 et supposons devoir calculer sa résistance équivalente.

On calcule tout d'abord la résistance équivalente (R2 - R3) aux résistances R2 et R3 en parallèle soit :
Aux deux résistances R2 et R3, on peut substituer une unique résistance de 20 Ohms (R2 et R3), comme dans la figure 7-b.
A partir de cette figure, on calcule la résistance (Req) équivalente (figure 7-c) à R1 et R2-3 en série :
De cet exemple pratique, il ressort qu'en présence d'un circuit complexe, il faut traiter les deux types d'associations séparément de manière à simplifier le circuit progressivement jusqu'à obtenir une unique résistance.
Il est également intéressant de voir le comportement des tensions et des courants dans un tel circuit.
Dans la figure 8 est reporté le même circuit mais complété par la représentation des différents courants et tensions .

Il nous faut à présent déterminer les paramètres accompagnés d'un point d'interrogation dans la figure 8 soit I, V1, V2, V3, I2 et I3.
I est le courant total circulant dans le circuit, nous l'obtenons en divisant la tension fournie par la pile par la résistance équivalente du circuit, qui est comme calculée précédemment de 25 Ohms :
V1, tension aux bornes de la résistance R1 s'obtient en multipliant R1 par le courant qui la traverse, or ce courant n'est autre que I :
V2-3, tension aux bornes de l'ensemble R2-R3 est égale à la différence entre la tension V de la pile et la tension V1 chutée par R1 :
I2, courant circulant dans R2 s'obtient en divisant la tension aux bornes de R2 soit V2-3 par R2 :
Le courant circulant dans R3, peut s'obtenir de deux façons :
Après avoir vu ce qui se produit dans le circuit extérieur des piles, selon le type de liaison adopté pour les résistances, nous allons examiner le circuit intérieur aux piles.
Le courant qui retourne aux pôles négatif de la pile, après avoir parcouru le circuit extérieur, doit traverser la solution électrolytique à l'intérieur de la pile pour se porter sur le pôle positif, d'où il recommence à circuler dans le circuit extérieur.
La solution électrolytique de la pile offre une résistance au courant qui la traverse. Comme cette résistance n'appartient pas au circuit extérieur, elle est appelée résistance interne de la pile.
Figure 9, la partie située à gauche des points A et B constitue le circuit interne de la pile.
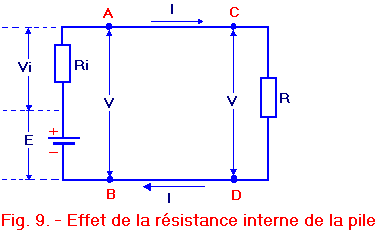
La pile possédant une résistance interne, il est possible de la matérialiser sur le circuit électrique, c'est ce que nous avons fait avec la résistance Ri.
Si nous considérons cette résistance Ri comme une résistance à part entière, étant traversée par le courant I, une tension Vi va naître à ses bornes. Ri produit une chute de tension mais comme Ri est située à l'intérieur de la pile, cette chute de tension s'effectue dans la pile. C'est pour cette raison que la résistance et la chute de tension qu'elle provoque sont symbolisées par un i, (i servant à rappeler que ces deux paramètres sont internes à la pile).
En conséquence, la tension nécessaire aux bornes de la pile n'est pas la tension totale fournie par la pile, mais est égale à cette tension diminuée de la chute de tension interne.
Selon la loi d'Ohm, la tension qui apparaît aux bornes de Ri s'obtient en multipliant Ri par le courant qui la traverse, or ce courant n'est autre que le courant traversant le circuit et fourni par la pile.
Nous constatons donc que la chute de tension interne à la pile est d'autant plus élevée que le courant débité par celle-ci augmente.
Inversement, cette chute de tension interne est nulle quand la pile n'est reliée à aucun circuit extérieur. Dans de telles conditions, aux bornes de la pile apparaît la totalité de la tension qu'elle peut fournir.
Cette tension s'appelle force électromotrice d'une pile et est symbolisée par la lettre E comme dans la figure 9.
Il faut retenir de ceci que la force électromotrice d'une pile est la tension présente à ses bornes lorsque la pile ne fournit aucun courant. L'unité de la force électromotrice est bien sûr le volt.
Dans la plupart des cas, la résistance interne d'une pile est de loin très inférieure à la résistance du circuit extérieur et lors d'éventuels calculs, cette valeur est négligée sans que cela apporte d'erreur appréciable dans les résultats.
Dans ces cas, nous considérons que la tension fournie par la pile est égale à sa force électromotrice. Dorénavant, pour le terme force électromotrice, nous utiliserons l'abréviation universellement reconnue f.e.m. (Nous reportons le même circuit pour vous faciliter la tâche).

Pour illustrer ce qui vient d'être dit, donnons des valeurs aux éléments de la figure 9 :
Le courant I circulant dans le circuit est donné par le rapport entre la f.e.m. et la résistance équivalente de ce circuit constitué de R et de Ri.
La chute de tension Vi interne à la pile est de :
La tension disponible aux bornes de la résistance R lorsque la pile débite un courant de 1 A est de :
Comme vous pouvez le constater, la tension chutée dans Ri est minime au regard de la tension réellement disponible aux bornes de R. Pour d'autres calculs, Vi pourrait donc être négligée.
Voyons à présent les différentes associations réalisables à partir de plusieurs piles.
Figure 10 est représenté le type d'association que vous serez appelé à rencontrer le plus souvent, il s'agit d'une association en série.
Cette association s'effectue en reliant la borne positive de l'une à la borne négative de l'autre. Puisque chaque pile a une f.e.m. de 1,5 V entre les points B et A, il y a une différence de potentiel de 1,5 V de même qu'entre les point C et B.
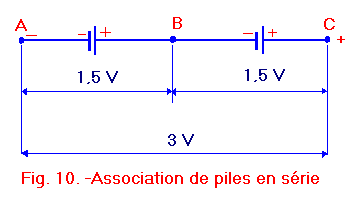
Le point C a un potentiel électrique supérieur de 1,5 V à celui du point B, qui lui-même a un potentiel supérieur de 1,5 V par rapport au point A. Nous aurons donc un potentiel électrique de 3 V entre les points C et A, bornes de l'ensemble.
Nous pouvons alors conclure :
En mettant plusieurs piles en série, on obtient une f.e.m. totale égale à la somme des f.e.m. de chaque pile.
On a recours à ce type d'association lorsque l'on a besoin d'une tension plus élevée que celle fournie par une seule pile. Dans ce cas, l'ensemble des piles reliées en série est aussi appelé batterie de piles. Ceci est le cas de la pile de 4,5 V que vous utilisez pour vos pratiques puisqu'elle est formée de trois éléments de 1,5 V chacun reliés en série.
En ce qui concerne la résistance interne, il est évident qu'une batterie de piles a une résistance interne égale à la somme des résistances internes de chaque élément qui la compose. Enfin, tous les éléments étant en série, ils sont traversés par le même courant, comme dans toutes les associations de ce type. D'autre part, il faut savoir qu'une pile ne doit jamais fournir un courant d'intensité supérieure à une valeur déterminée, qui dépend de ses caractéristiques de fabrication, sous peine d'entraîner rapidement sa détérioration.
C'est pour cela que le circuit extérieur d'une pile n'est jamais constitué par un simple fil de cuivre : en effet, à cause de la très faible résistance du fil, la pile serait obligée de fournir un courant d'intensité très élevée qui la détériorerait très vite. Dans ce cas, on dit que la pile est en court-circuit ; pour la bonne conservation des piles, il faut donc éviter de les mettre en court-circuit, en reliant directement leurs pôles par un simple conducteur de résistance négligeable.
Quand un courant plus important que celui que peut délivrer une seule pile est nécessaire, nous utilisons plusieurs piles reliées en parallèle comme le montre la figure 11.

Dans cette figure, nous voyons que le courant total fourni par plusieurs piles en parallèle est égal à la somme des courants que peut fournir chaque pile.
Naturellement, pour que cela se produise, il faut que les pôles positifs de chaque pile soient reliés entre eux, de même que les pôles négatifs, comme sur la figure 11. Aux bornes de l'ensemble, la f.e.m. est égale à celle fournie par une seule pile, caractéristique commune à toutes les associations en parallèle.
En pratique, ce type d'association est rarement utilisé parce que si les résistances internes et les f.e.m. de chaque pile ne sont pas rigoureusement identiques, on observera la décharge d'une pile dans l'autre entraînant leur détérioration mutuelle.