

IMPÉDANCE ÉLECTRIQUE

Cette leçon traite, dans un premier temps, de l'impédance électrique d'une bobine inductrice.
Dans un second chapitre, nous allons examiner la puissance électrique en courant alternatif.
Enfin, la dernière partie est consacrée à l'analyse des circuits magnétiques.

Nous allons commencer cette nouvelle théorie en examinant les inductances.
Une inductance, ou bobine, est un enroulement constitué de nombreuses spires d'un fil conducteur, généralement de faible section.
Ces inductances sont des obstacles au passage du courant. Si le courant considéré est continu, on dit qu'elles offrent une résistance ; s'il est alternatif, on parle alors de réactance et, plus précisément dans le cas des inductances, de réactance inductive.
La résistance est une grandeur que nous connaissons déjà. C'est la résistance ohmique du conducteur. Son symbole est évidemment R et elle s'exprime en ohms.
La réactance, qui n'apparaît que lorsque la bobine est parcourue par un courant alternatif, est fonction d'une caractéristique propre de la bobine, appelée coefficient de self-induction et symbolisé par la lettre L, et de la fréquence du courant alternatif. Comme la résistance, elle s'exprime en ohms.
Lorsque la valeur de la résistance est faible par rapport à celle de la réactance, on la néglige. Dans ce cas, l'inductance est représentée schématiquement comme le montre la figure 1-a.
Si l'on veut au contraire considérer la valeur de la résistance R, le schéma équivalent de l'inductance est celui représenté figure 1-b.

Le symbole d'une inductance résistive permet de considérer l'inductance réelle comme étant constituée d'une inductance sans résistance ohmique (L) associée en série avec une résistance pure (R).
Les bornes réelles de l'inductance résistive sont A et B (figure 1-b). La tension V, appliquée aux bornes A et B, se répartit aux bornes de L et de R qui forment un diviseur de tension. On obtient ainsi aux bornes de chacun de ces éléments les tensions VL et VR.
On pourrait donc penser qu'entre les extrémités A et B de l'inductance, il faut appliquer une tension V dont la valeur efficace est la somme des valeurs efficaces de VL et de VR.
En fait, il n'en est pas ainsi car les tensions VL et VR n'ont pas la même phase par rapport au courant comme le montre la figure 2.
Deux périodes (ou cycles) du courant sont représentées figure 2-a, la deuxième est représentée par un trait plus accentué. La tension VR, nécessaire pour la partie résistive, est représentée figure 2-b, durant deux périodes également.

Il apparaît que VR est en phase avec le courant I. La tension VL est représentée figure 2-c.
Le trait gras indique une période (ou un cycle) complète. Cette tension VL est déphasée d'un quart de période par rapport à VR ou à I.
Elle débute un quart de période avant VR et se termine également un quart de période avant VR.
Ainsi, la tension VL apparaissant aux bornes de la bobine (inductance) est déphasée en avance d'un quart de période par rapport à la tension VR.
Par suite de ce déphasage, à l'instant où l'une des deux tensions atteint la valeur maximale, l'autre atteint la valeur zéro et inversement ; en effet, en comparant les figures 2-b et 2-c, on s'aperçoit, par exemple, qu'au temps 0 seconde correspondent les tensions VR nulle et VL maximale ; au contraire, au temps de 0,05 seconde correspondent une tension VL nulle et une tension VR maximale.
Au temps 0 seconde, la tension V appliquée entre les extrémités A et B de la bobine est égale à la valeur maximale de VL puisque VR est nulle à cet instant. Par contre, au temps 0,05 seconde, V est égale à la valeur maximale de VR puisque VL est nulle.
La valeur maximale de V n'est donc pas égale à la somme des valeurs maximales des tensions VL et VR car ces deux valeurs maximales sont atteintes à des instants différents.
Pour calculer la tension V, il faut avoir recours à la représentation vectorielle, qui permet de mettre en évidence le déphasage entre VL et VR.
La figure 3 représente vectoriellement les tensions VR, VL et le courant I. Ces représentations sont les mêmes que celles déjà vues pour le circuit ohmique et pour le circuit inductif.
Les éléments L et R étant en série, ils sont parcourus par le même courant I. Nous prendrons donc le vecteur représentant ce courant comme vecteur de référence.
Nous savons que dans une résistance pure, courant et tension sont en phase. Les deux vecteurs les représentant seront donc sur le même axe (figure 3-a).

Nous venons de voir que dans une inductance pure, la tension VL est déphasée d'un front de période en avance sur VR. Comme VR est en phase avec I, on peut également dire que VL est en avance sur IR. Un quart de période correspondant à 90°, la représentation vectorielle de VL par rapport à I sera celle de la figure 3-b.
Nous pouvons enfin représenter sur un même graphique les différentes valeurs représentées figure 3-a et 3-b. Nous obtenons ainsi la figure 3-c.
Pour trouver le vecteur représentant la tension V, il faut effectuer la somme vectorielle des deux vecteurs représentant VR et VL. On tient ainsi compte des valeurs maximales de VR et VL et du déphasage entre ces deux tensions.
La figure 4-a, indique la somme des deux vecteurs VL et VR. Nous remarquons que le sens, la direction et la longueur des vecteurs sont identiques à ceux de la figure 3-c. Le déphasage est toujours égal à 90°. Il suffit de réunir les extrémités O et A des deux vecteurs pour obtenir celui représentant la tension V.
.gif)
Pour calculer la valeur de V, il suffit de tenir compte du fait qu'un centimètre représente 10 volts.
(Si vous avez oublié ce théorème de Pythagore, cliquez sur le lien ci-contre). Théorème de Pythagore.
Le vecteur VL (2 cm de long) représente une tension de 20 volts, tandis que le vecteur VR (3 cm de long) représente une tension de 30 volts.
En mesurant sur la figure la longueur du vecteur V, nous voyons qu'elle est de 3, 6 cm et que, par conséquent, la tension V vaut 36 volts.
Nous pouvons conclure que la tension V à appliquer aux bornes de la bobine pour qu'elle soit parcourue par un courant de 1 A, a la valeur maximale de 36 volts.
Il est également possible de calculer cette valeur en appliquant le théorème de Pythagore au triangle rectangle formé par les trois vecteurs.
Faisons un bref rappel de ce théorème à l'aide de la figure 4-b.
Les côtés AB et AC sont les côtés de l'angle droit ; BC, qui est le plus long, est l'hypoténuse.
Selon le théorème de Pythagore, en faisant la somme des carrés des longueurs des côtés de l'angle droit, on obtient le carré de la longueur de l'hypoténuse.
Dans le cas de la figure 4-b, on a :
Ce théorème peut être appliqué au schéma de la figure 4-a :
Ce nombre 1 300, est donc le carré de la valeur maximale de V.
La racine carrée de 1 300 est 36,055. Nous retrouvons bien la même valeur que celle mesurée précédemment (36 volts).
Nous savons que la valeur maximale d'une tension alternative est égale à 1,41 fois sa valeur efficace.
Nous pouvons donc dire que la valeur efficace de la tension que l'on doit appliquer aux extrémités d'une bobine est égale à la racine carrée du nombre obtenu en faisant la somme des carrés des valeurs efficaces des tensions nécessaires pour la partie inductive et pour la partie ohmique de cette bobine.
Nous avons déjà dit que la partie résistive et la partie inductive constituent un obstacle au passage du courant dans la bobine. Cet obstacle est appelé impédance électrique et on l'indique symboliquement par la lettre Z.
L'impédance électrique se mesure en ohms, comme la résistance et la réactance.
Cette impédance s'exprime par la relation suivante :

XL est la réactance de la partie inductive. Pour déterminer cette relation, il faut partir de la relation : V2 = VR2 + VL2 (application du théorème de Pythagore).

Ainsi, la loi d'OHM s'applique à une bobine résistive, tout comme elle s'appliquait à une résistance et à une inductance pure.
La valeur de la tension nécessaire pour qu'un courant alternatif déterminé traverse une bobine s'obtient en multipliant ce courant par l'impédance qu'elle présente.
Il nous reste à voir le déphasage existant entre cette tension et le courant.
(Pour en faciliter la lecture, nous reportons le même schéma à savoir figure 4) :
.gif)
Sur la figure 4-a, pour trouver le vecteur V, nous avons dessiné le vecteur VR horizontalement, puis le vecteur VL verticalement, à l'extrémité de VR.
Nous pouvons également adopter la procédure indiquée figure 5-a, c'est-à-dire dessiner horizontalement le vecteur VR puis verticalement le vecteur VL. En reliant ensuite les points O et A, on obtient le vecteur V en tout point identique à celui de la figure 4-a.
Le vecteur V peut aussi se déduire directement de la figure 3-c, ce qui est indiqué figure 5-b.

Pour situer le point A, il suffit de tracer deux parallèles aux vecteurs VL et VR ; elles sont indiquées en pointillé sur cette figure 5-b. Cette nouvelle méthode présente l'avantage de mettre en évidence le déphasage existant entre V et I.
Ce déphasage correspond
à l'angle ![]() "phi" (
"phi" ( ![]() est la lettre
minuscule qui correspond à la lettre
est la lettre
minuscule qui correspond à la lettre ![]() qui est une
lettre majuscule de l'alphabet grec). Nous notons que cet angle
qui est une
lettre majuscule de l'alphabet grec). Nous notons que cet angle ![]() est
inférieur à 90°.
est
inférieur à 90°.
Cela signifie qu'une bobine
résistive possède des caractéristiques
intermédiaires entre celles d'une résistance
pure ( ![]() = 90°).
= 90°).
L'angle de déphasage est donc proportionnel au rapport de la réactance sur la résistance.
La figure 5-c représente ce
déphasage dans le cas où la réactance est
très supérieure à la résistance. Dans ce
cas, l'angle ![]() est proche de
90°.
est proche de
90°.
Sur la figure 5-d, c'est le cas
contraire qui est représenté ; l'angle ![]() est proche de
0° car la réactance est très faible par rapport
à la valeur de la résistance.
est proche de
0° car la réactance est très faible par rapport
à la valeur de la résistance.

Dans un circuit parcouru par un courant continu, la puissance P qu'il dissipe s'exprime par la relation : P = V x I.
Dans un circuit parcouru par un courant alternatif, la tension et l'intensité varient à chaque instant, et la puissance instantanée s'exprime par la relation p = v x i ("v" est la tension instantanée et "i" l'intensité instantanée).
Pour déterminer la puissance dans un circuit, il faut alors considérer trois cas.
2. 1. - PREMIER CAS : LA TENSION ET LE COURANT SONT EN PHASE
C'est le cas d'un circuit purement résistif. La tension et le courant ont l'allure représentée figure 6-a.

Pour obtenir la courbe représentative de la puissance (figure 6-b), il suffit de multiplier point par point la valeur de la tension (v) par celle de l'intensité i.
Cette courbe est une sinusoïde située entièrement au-dessus de l'axe des abscisses puisque le produit (vi) est toujours positif. Par contre, la fréquence de cette sinusoïde est le double de celle de (v) ou de i.
La puissance (p) est égale à 0 quand v = i = 0. Elle est maximale quand (v) et (i) sont maximums.
La valeur moyenne (P) de la puissance considérée correspond à la moitié de Pmax, soit :

Cette relation est identique à celle obtenue dans le cas d'un courant continu.
Puisque la puissance en jeu dans le circuit résistif peut être utilisée afin de produire un travail, elle est appelée puissance active. Elle se mesure en watts et se désigne par le symbole P.
2. 2. - DEUXIÈME CAS : LA TENSION ET LE COURANT SONT DÉPHASES DE 90°
Considérons le cas d'une inductance pure.
La tension (v) est en avance de 90° par rapport à l'intensité (i) comme représenté figure 7-a.
Comme dans le cas précédent, il suffit de multiplier à chaque instant la tension (v) par l'intensité (i) pour obtenir la courbe représentative de la puissance P (figure 7-b).

Nous remarquons que la sinusoïde résultante est la même que celle de la figure 6-b, mais cette fois-ci, elle est centrée sur l'axe des abscisses. En effet, dans le premier quart de période, la tension comme l'intensité sont positives ; la puissance l'est donc aussi. Dans le second quart de période, l'intensité reste positive, mais la tension devient négative, la puissance est donc négative. On peut faire une analyse similaire pour les troisième et quatrième quarts de période.
La valeur moyenne de la puissance est nulle. Si l'on veut calculer l'énergie dépensée dans l'inductance pure, on trouve qu'elle est nulle puisque la puissance est nulle.
Cela paraît contradictoire avec le principe selon lequel un générateur fournit de l'énergie au circuit récepteur qui lui est relié.
Nous savons que pour un circuit résistif, l'énergie consommée est transformée et dissipée sous forme de chaleur.
Dans le cas d'un circuit purement inductif, l'énergie fournie par le générateur est emmagasinée dans le champ magnétique créé par l'inductance quand le courant augmente.
Ce champ magnétique se dissipe quand le courant diminue et l'énergie fournie antérieurement est restituée au générateur.
La puissance mise en jeu dans un circuit purement inductif étant nulle, elle ne produit aucun travail. On l'appelle la puissance réactive. On la désigne par le symbole Q (on trouve également Pr) et on la mesure en volts ampères réactifs (VAR).
2. 3. - TROISIÈME CAS : LA TENSION ET LE COURANT SONT
DÉPHASÉS D'UN ANGLE ![]() COMPRIS ENTRE
0° ET 90°
COMPRIS ENTRE
0° ET 90°
C'est le cas le plus général.
Le courant et la tension sont alors
représentés par deux vecteurs V et
I
déphasés entre eux d'un certain angle ![]() , comme
illustré figure 8-a.
, comme
illustré figure 8-a.
Pour trouver la puissance active P absorbée par le circuit, décomposons le vecteur I en deux vecteurs : le premier IA en phase avec la tension V et le second IQ déphasé de 90° comme illustré figure 8-b.
On peut imaginer que le circuit est parcouru par deux courants distincts (IA et IQ) déphasés entre eux de 90°.

Le courant IQ est déphasé de 90° par rapport à la tension V. Ce courant IQ n'accomplit aucun travail utile. Il détermine seulement un échange alterné d'énergie entre le générateur et le circuit.
C'est uniquement le courant IA en phase avec la tension V qui produit un travail utile.
Le produit de la tension V par le courant I représente donc une puissance apparente absorbée par le circuit inductif et résistif. Une partie seulement de cette puissance apparente, notée S, est utilisée par le circuit en fournissant un travail utile.
Cette puissance apparente (S) s'exprime en volts ampères (VA).
Les trois puissances (active, réactive et apparente) sont liées par une relation que l'on peut déduire de la figure 9.
Ces trois vecteurs représentant les trois puissances forment un triangle rectangle. L'hypoténuse représente la puissance apparente S et les deux côtés représentent respectivement la puissance active P et la puissance réactive Q.

A l'aide des relations trigonométriques, on déduit :

Le facteur cos ![]() représente la fraction (inférieure
à 1) de la puissance apparente (S) effectivement
utilisée par le circuit.
représente la fraction (inférieure
à 1) de la puissance apparente (S) effectivement
utilisée par le circuit.
Ce facteur cos ![]() est appelé facteur de puissance
du
circuit et s'exprime par la relation :
est appelé facteur de puissance
du
circuit et s'exprime par la relation :
Nous pouvons également exprimer ces puissances sous une autre forme. Nous avons vu que la puissance apparente est le produit de la tension V par le courant I. Nous pouvons donc écrire :
Nous pouvons alors inscrire cette valeur dans le triangle des puissances (figure 10).
Nous venons de voir que la puissance active P est donnée par la relation :
En remplaçant S par sa valeur VI, nous obtenons :

D'autre part, la puissance réactive Q nous est donnée par la relation :
Qui devient :

Une bobine (inductance) doit généralement posséder une inductance (L) élevée par rapport à sa partie résistive R. Pour cela, une bobine est munie d'un noyau ferromagnétique.
En effet, dans les théories précédentes, il a été noté que la valeur de l'inductance pour une bobine est aussi en fonction du matériau situé à l'intérieur de celle-ci. Le noyau ferromagnétique permet donc d'augmenter notablement l'inductance, tout en conservant la valeur de la résistance constituée par l'enroulement du fil.
Pour obtenir une inductance élevée, il faut que le noyau soit fermé sur lui-même de façon que l'ensemble des lignes d'induction soit contenu dans le noyau.
En examinant la bobine de la figure 11-a, on s'aperçoit que les lignes d'induction se referment à l'extérieur du noyau en passant par les couches d'air extérieures à ce dernier.

Il suffit de refermer progressivement le noyau sur lui-même (figure 11-b) jusqu'à ce que les deux extrémités soient en contact (figure 11-c) pour que toutes les lignes d'induction soient «emprisonnées» dans le noyau.
Ainsi, on a obtenu un noyau fermé, qui est traversé par la totalité du flux d'induction produit par la bobine. Aucune ligne d'induction ne peut se refermer dans l'air.
L'inductance résultante est égale au produit de l'inductance sans noyau par la perméabilité relative du matériau constituant le noyau ferromagnétique.
Pour des raisons de fabrication, les noyaux utilisés en pratique n'ont généralement pas la forme illustrée figure 11-c, mais la forme «à colonne» (figure 12-a), ou la forme «cuirassée ou blindée» (figure 12-b), qui est la plus utilisée.
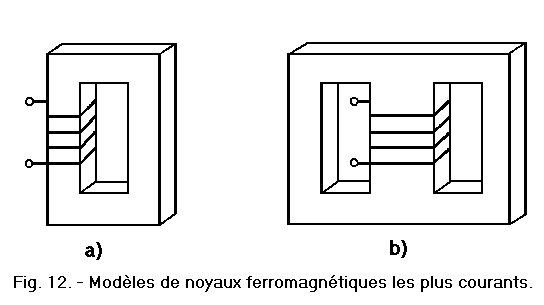
Nous pouvons noter par ailleurs que l'enroulement n'effectue pas le tour complet du noyau, mais se situe seulement dans une de ses parties rectilignes.
Cela est lié au mode de fabrication de la bobine. Dans un premier temps, seul l'enroulement du fil est réalisé et dans un second temps, la carcasse métallique constituée de feuilles est assemblée avec l'enroulement de la bobine.
Comme l'indique la figure 13, le flux d'induction se referme presque totalement dans le noyau. Seules, quelques lignes d'induction tracées en pointillé sortent du noyau.
Pour expliquer le fait que les lignes d'induction restent à l'intérieur du noyau, il faut imaginer que le noyau ferromagnétique est constitué d'aimants élémentaires très petits et mis bout à bout. Ainsi, les lignes d'induction suivent exactement l'orientation privilégiée de ces petits aimants dans le noyau.

Puisque les lignes d'induction passent préférentiellement dans le noyau, nous disons que le noyau est plus perméable que l'air aux lignes d'induction.
Une image peut être donnée en imaginant un terrain perméable à l'eau entouré par un terrain imperméable. Le terrain central perméable représente le noyau, le terrain extérieur imperméable représente l'air entourant le noyau.
Quand la pluie tombe, il est bien évident que c'est le terrain central, perméable qui absorbe l'essentiel de l'eau. Il en est de même avec les lignes d'induction et le noyau ferromagnétique. Pour cette raison, on emploie le terme de «perméabilité magnétique» pour un matériau déterminé.
Par rapport à l'air, le noyau ferromagnétique détermine une augmentation de l'inductance, ou du flux d'induction, précisément parce qu'il est plus facilement traversé par les lignes d'induction que l'air.
Le second avantage dans l'emploi d'un noyau réside dans le fait que ce noyau canalise les lignes d'induction, c'est-à-dire qu'il les contraint à parcourir un «chemin» obligatoire.
Les lignes d'induction quittant le parcours imposé par le noyau constituent le flux de dispersion.
Ce flux de dispersion peut généralement être négligé devant le flux d'induction dans le cas d'une bobine avec noyau.
Comme le montre la figure 13 ci-dessus, l'enroulement et le noyau refermé sur lui-même présentent des analogies avec un circuit électrique. L'ensemble est donc appelé circuit magnétique.
Pour chaque type de circuit magnétique, on peut trouver le circuit électrique correspondant : par exemple, le circuit magnétique de la figure 13-a correspond au circuit électrique de la figure 13-c constitué par un conducteur de résistance non négligeable relié à une pile.
Comme la f.e.m. (E) fait circuler un courant
(I)
dans le conducteur, on peut dire que la f.m.m. (force
magnétomotrice) "N.I." fait traverser le
noyau par le flux d'induction ![]() .
.
En considérant le circuit électrique analogue à un circuit magnétique donné, l'examen de ce dernier peut se trouver facilité. Par exemple, au circuit magnétique de la figure 13-b correspond le circuit électrique de la figure 13-d. Ce dernier est constitué de deux conducteurs de résistance identique mis en parallèle et reliés à la pile. Le courant (I) fourni par la pile se subdivise en deux parties égales I / 2 dans chaque conducteur.
Le flux d'induction dans un circuit
magnétique correspondant présente un comportement
analogue. En effet, le flux ![]() produit par la bobine se partage en deux flux égaux
indiqués par
produit par la bobine se partage en deux flux égaux
indiqués par ![]() / 2 figure
13-b, chacun traversant une des branches latérales du
noyau.
/ 2 figure
13-b, chacun traversant une des branches latérales du
noyau.
On peut poursuivre l'analogie entre circuits magnétiques et circuits électriques. Pour un circuit électrique, quand on divise le f.e.m. par le courant, on obtient la résistance (loi d'OHM) du circuit. Pour un circuit magnétique, si l'on divise la f.m.m. par le flux d'induction, on obtient une grandeur analogue à la résistance du circuit électrique ; il s'agit de la réluctance magnétique du noyau. Le symbole est R et cette réluctance s'exprime en 1 / H.
La réluctance magnétique indique le nombre d'ampères-tours nécessaires pour obtenir un flux d'induction d'un Weber (Wb).
Comme la résistance est fonction de la longueur et de la section pour un conducteur donné, la réluctance est fonction de celles du noyau.
La réluctance est proportionnelle à la longueur du noyau et inversement proportionnelle à sa section.
De même que la résistivité intervient dans le calcul de la résistance électrique d'un matériau donné, la perméabilité absolue intervient pour le calcul de la réluctance d'un noyau ferromagnétique.
Plus la perméabilité du noyau est élevée, plus le flux d'induction est élevé et plus la réluctance sera faible.
En conclusion, on peut dire que la réluctance d'un noyau ferromagnétique s'obtient en divisant sa longueur par sa section et par sa perméabilité absolue.
Les circuits magnétiques considérés jusqu'à présent sont fermés (leur noyau est fermé sur lui-même).
Notons qu'il existe des circuits ouverts. Dans ce cas, le noyau possède un entrefer comme cela apparaît figure 14-a. Cet entrefer est une petite région de l'espace où le noyau se trouve interrompu.
La direction des lignes d'induction n'est pratiquement pas modifiée par cet entrefer.

Si l'on connaît la section et la longueur de l'entrefer ainsi que la perméabilité magnétique de l'air, on peut calculer la réluctance présentée au flux d'induction dans l'entrefer. Cette réluctance de l'entrefer est plus élevée que celle d'un noyau ferromagnétique de mêmes dimensions que l'entrefer.
Ce nouveau circuit magnétique est analogue au circuit de la figure 14-b. La résistance R possède une valeur résistive bien plus élevée que les conducteurs qui relient à la pile.
Cette résistance R est analogue à l'entrefer du circuit magnétique tandis que les deux conducteurs électriques sont analogues au noyau ferromagnétique.
La réluctance totale du circuit magnétique est égale à la somme de la réluctance du noyau et de celle de l'entrefer.
Après avoir montré ces analogies entre un circuit magnétique et un circuit électrique, il convient d'en présenter les différences.
Comme nous le savons, le courant qui parcourt un circuit électrique est proportionnel à la f.e.m., or il n'en est pas de même pour un circuit magnétique, il n'y a plus proportionnalité entre la f.m.m. et le flux d'induction.
Dans certaines conditions, pour une augmentation de la f.m.m., le flux d'induction ne varie pas.
Ce fait est dû à la présence du noyau et il faut donc considérer le comportement du matériau constitutif du noyau en relation avec les variations de la f.m.m..
Pour examiner le comportement d'un matériau ferromagnétique déterminé, on construit un noyau avec lui puis on dispose une bobine autour de ce noyau. On fait circuler un courant (I) progressivement croissant de façon à augmenter la f.m.m. (N x I).
Pour chaque courant I, on mesure le flux d'induction à l'aide d'un fluxmètre. Cela permet de tracer une courbe représentant le flux d'induction en fonction de la f.m.m. (N x I).
Les valeurs de la f.m.m. sont reportées sur
l'axe horizontal d'un repère cartésien. Les valeurs du
flux ![]() sont
reportées sur l'axe vertical.
sont
reportées sur l'axe vertical.
La figure 15-a représente cette courbe pour
un matériau ferromagnétique courant. Au début,
au point O, la f.m.m. est nulle ainsi que le flux ![]() ; puis la f.m.m. augmente, on constate que
le flux
; puis la f.m.m. augmente, on constate que
le flux ![]() augmente
également, dans un premier temps relativement peu (au
début de la courbe), puis dans un deuxième temps,
beaucoup plus ;
dans un troisième temps, quand on approche du point A, la
variation du flux
augmente
également, dans un premier temps relativement peu (au
début de la courbe), puis dans un deuxième temps,
beaucoup plus ;
dans un troisième temps, quand on approche du point A, la
variation du flux ![]() diminue
nettement jusqu'à s'annuler pratiquement au-delà du
point A.
diminue
nettement jusqu'à s'annuler pratiquement au-delà du
point A.
Au point A, il y a saturation magnétique. On dit qu'au-delà du point A, le noyau est saturé. En effet, plus la f.m.m. augmente, plus le nombre d'aimants élémentaires qui constituent le noyau s'oriente dans la direction des lignes d'induction.

Quand on arrive au point A, tous les aimants
élémentaires sont orientés et par
conséquent, le flux ![]() ne
peut s'accroître.
ne
peut s'accroître.
La courbe de la figure 15-a est la courbe de première magnétisation car elle est obtenue quand on magnétise pour la première fois un noyau ferromagnétique.
Maintenant, il nous faut envisager le cas d'une bobine avec noyau parcourue par un courant alternatif. Pour cela, partons du point A au point de saturation précédemment décrit.
On pourrait penser que lorsque la f.m.m. diminue,
le flux ![]() reprend les
mêmes valeurs que précédemment, or il n'en est
rien.
reprend les
mêmes valeurs que précédemment, or il n'en est
rien.
Sur la figure 15-b, on voit que le flux ![]() du point A au point B prend des
valeurs supérieures à celles relatives à la
première magnétisation.
du point A au point B prend des
valeurs supérieures à celles relatives à la
première magnétisation.
En particulier, quand le courant devient nul, nous voyons que le flux ne l'est pas (point B).
Il s'agit du flux résiduel ou flux rémanent.
Au-delà du point O, vers la gauche, les valeurs de la f.m.m. deviennent négatives, c'est-à-dire que le courant I a changé de sens. (Figure 15-c).
On s'aperçoit que lorsque la f.m.m. atteint
une certaine valeur négative (point C), le flux ![]() devient nul.
devient nul.
Nous voyons ainsi que pour annuler le flux résiduel, il faut faire circuler dans l'enroulement de la bobine un certain courant dirigé en sens contraire à celui ayant servi à magnétiser le noyau.
On peut dire que le flux d'induction suit les variations du courant alternatif avec un certain retard. Ce phénomène constitue l'hystérésis magnétique (hystérésis signifie retard).
Si la f.m.m. continue d'augmenter, le courant étant toujours dans le sens contraire à celui de la première magnétisation, le flux augmente (courbe du point C au point D) mais il a changé de sens par rapport à celui de la première magnétisation.
Quand on parvient au point D, le noyau est saturé, tous les aimants élémentaires se sont orientés dans le sens contraire à celui de la première magnétisation.
Lorsque le courant diminue à nouveau
jusqu'à s'annuler, le flux ![]() décroît du point D au point E. Donc il existe encore un
flux rémanent égal en intensité à celui
vu précédemment mais de sens contraire.
décroît du point D au point E. Donc il existe encore un
flux rémanent égal en intensité à celui
vu précédemment mais de sens contraire.
Lorsque la f.m.m. augmente à nouveau, on passe du point E au point F (flux nul) puis on rejoint le point A de saturation. Ainsi, on a accompli un cycle complet d'hystérésis.
Les flèches sur la figure 15-c indiquent le sens de parcours du cycle.
Pour toute bobine possédant un noyau ferromagnétique et parcourue par un courant alternatif, il existe un tel cycle d'hystérésis dans le noyau. C'est le cas, en particulier, des transformateurs d'alimentation qui seront l'objet de la prochaine théorie, mais avant tout, nous allons continuer l'étude des transistors.
